数据来源：tushare A股日线行情

1
2
3
4
5
6
7
8
9
10
11
import tushare as ts
import numpy as np
# 设置tushare的token
ts.set_token('4e542e2517c15f3ef8b5d5f53c50ed43b501c0952dfeeda41dbdbd4e')
# 初始化pro接口
pro = ts.pro_api()

from matplotlib import font_manager
# 设置中文字体 Linux系统 宋体
font = font_manager.FontProperties(fname="/usr/share/fonts/Fonts/simsun.ttc")
import matplotlib.pyplot as plt

交易日每天15点～16点之间入库，使用5家上市企业8月1日到9月1日的A股日线行情深圳证券交易所数据。

1
2
3
4
5
6
7
8
9
10
11
12
# 导入数据
data1=pro.daily(ts_code='002594.SZ',start_date='20240801',end_date='20240901')#比亚迪
qiye1=np.array(data1['close'])
data2=pro.daily(ts_code='300124.SZ',start_date='20240801',end_date='20240901')#/汇川技术
qiye2=np.array(data2['close'])
data3=pro.daily(ts_code='002460.SZ',start_date='20240801',end_date='20240901')#赣锋锂业
qiye3=np.array(data3['close'])
data4=pro.daily(ts_code='300750.SZ',start_date='20240801',end_date='20240901')#宁德时代
qiye4=np.array(data4['close'])
data5=pro.daily(ts_code='300014.SZ',start_date='20240801',end_date='20240901')#亿纬锂能
qiye5=np.array(data5['close'])

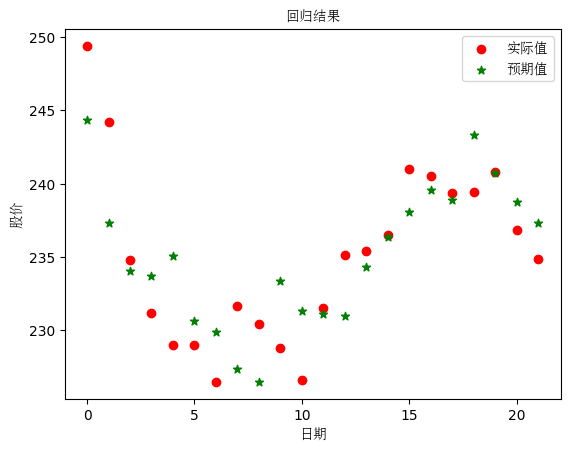
一、 最小二乘法

使用 sklearn 的 linear_model.LinearRegression() 包，以四家企业股票数据作为输入数据 X，以比亚迪股票数据作为 y，预测比亚迪股票。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

from sklearn import linear_model
# 创建线性回归模型
reg = linear_model.LinearRegression()
x=[]
y=[]
for i in range(len(qiye1)):
    x.append([qiye2[-i],qiye3[-i],qiye4[-i],qiye5[-i]])
    y.append(qiye1[-i])

# 根据参数拟合直线
reg.fit(x,y)

# 线性回归问题的估计系数
print(reg.coef_)

# 决策函数中的独立项
print(reg.intercept_)

#画图
plt.scatter(range(len(qiye1)),y,c="red", marker='o', label='实际值')
plt.scatter(range(len(qiye1)),reg.predict(x), c="green", marker='*', label='预期值')
plt.xlabel('日期', fontproperties=font)
plt.ylabel('股价', fontproperties=font)
plt.legend(prop=font)
plt.title("回归结果", fontproperties=font)
plt.show()
[-1.10978233  4.1781369   0.83544054 -0.43331279]
38.73142244793675

png

二、 梯度下降法

实验原理

使用sklearn 的 linear_model.SGDRegressor 包，以四家企业股票数据作为输入数据 X，以比亚迪股票数据作为 y，预测比亚迪股票。

实验细节

学习率设置为0.0001

划分数据集

1
2
3
4
X_train_sta = standardScaler.fit_transform(X[0:-10])
X_test_sta = standardScaler.transform(X[-10:])
y_train_sta = y[0:-10]
y_test_sta = y[-10:]

将数据的后10维作为验证集，将之前的数据分为训练集，对训练集归一化，进行训练。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler

# 标准化数据
standardScaler = StandardScaler()
X_train_sta = standardScaler.fit_transform(x[0:-10])  # 对训练集进行标准化
X_test_sta = standardScaler.transform(x[-10:])  # 对测试集进行标准化
y_train_sta = y[0:-10]  # 训练集的目标值
y_test_sta = y[-10:]  # 测试集的目标值

# 创建随机梯度下降回归模型
sgd_reg = SGDRegressor(alpha=0.0001)

# 使用训练集数据拟合模型
sgd_reg.fit(X_train_sta, y_train_sta)

# 输出模型在测试集上的得分
print(sgd_reg.score(X_test_sta, y_test_sta))

# 输出回归问题的估计系数
print(sgd_reg.coef_)

# 输出模型的详细信息
print(sgd_reg)

# 可视化回归结果
plt.scatter(range(10), y_test_sta, c="red", marker='o', label='实际值')  # 画出实际值
plt.scatter(range(10), sgd_reg.predict(X_test_sta), c="green", marker='*', label='预期值')  # 画出预测值
plt.xlabel('日期', fontproperties=font)  # 设置x轴标签
plt.ylabel('股价', fontproperties=font)  # 设置y轴标签
plt.legend(prop=font)  # 设置图例
plt.title("回归结果", fontproperties=font)  # 设置标题
plt.show()  # 显示图像
-18.168003628434395
[ 0.84155388 -1.30852736  4.97132202 -2.00460589]
SGDRegressor()

png

实验结果

回归系数为：[ 0.74271056 -1.21307246 4.97542077 -1.95273362]

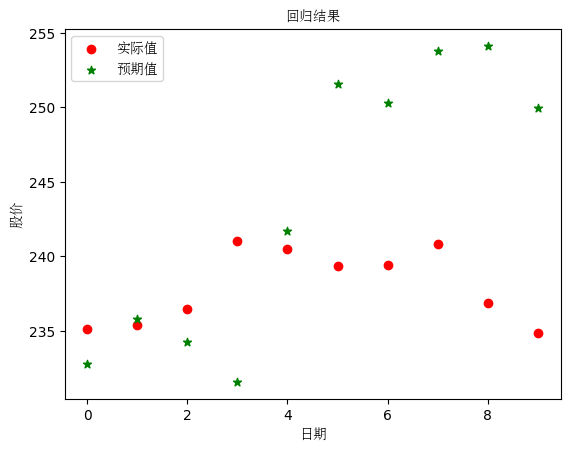
实验结果可视化：

将测试集与预测结果表示在图中，红点为比亚迪连续十天股票，绿色为股票预测值，可以看出相关性较强。

三、 牛顿法

实验思路

随机初始化数据，使用牛顿法拟合函数

数据为：

1
2
X1 = np.arange(-1.5, 1.5 + 0.05, 0.05)
X2 = np.arange(-3.5, 2 + 0.05, 0.05)

实际函数：

1
f = 100 * (x2 - x1 ** 2) ** 2 + (1 - x1) ** 2  # 给定的函数

预测函数表达式：

1
fun = lambda x: 100 * (x[0] ** 2 - x[1]) ** 2 + (x[0] - 1) ** 2

梯度向量：

1
gfun = lambda x: np.array([400 * x[0] * (x[0] ** 2 - x[1]) + 2 * (x[0] - 1), -200 * (x[0] ** 2 - x[1])])

海森矩阵：

1
hess = lambda x: np.array([[1200 * x[0] ** 2 - 400 * x[1] + 2, -400 * x[0]], [-400 * x[0], 200]])

初始点设置为：

1
x0 = np.array([-1.2, 1])

最大迭代次数：

1
maxk = 500

迭代结束条件：

1
epsilon = 1e-5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import random
def dampnm(fun, gfun, hess, x0):
    # 用牛顿法求解无约束问题
    # x0是初始点，fun，gfun和hess分别是目标函数值，梯度，海森矩阵的函数
    maxk = 500
    rho = 0.55
    sigma = 0.4
    k = 0
    epsilon = 1e-5

    with open("牛顿.txt", "w") as f:
        W = np.zeros((2, 20000))

        while k < maxk:
            W[:, k] = x0
            gk = gfun(x0)
            Gk = hess(x0)
            dk = -1.0 * np.linalg.solve(Gk, gk)
            print(k, np.linalg.norm(dk))
            f.write(str(k) + '   ' + str(np.linalg.norm(gk)) + "\n")
            if np.linalg.norm(dk) < epsilon:
                break

            x0 += dk
            k += 1
        W = W[:, 0:k + 1]  # 记录迭代点
        return x0, fun(x0), k, W


# 函数表达式fun
fun = lambda x: 100 * (x[0] ** 2 - x[1]) ** 2 + (x[0] - 1) ** 2

# 梯度向量 gfun
gfun = lambda x: np.array([400 * x[0] * (x[0] ** 2 - x[1]) + 2 * (x[0] - 1), -200 * (x[0] ** 2 - x[1])])

# 海森矩阵 hess
hess = lambda x: np.array([[1200 * x[0] ** 2 - 400 * x[1] + 2, -400 * x[0]], [-400 * x[0], 200]])




X1 = np.arange(-1.5, 1.5 + 0.05, 0.05)
X2 = np.arange(-3.5, 2 + 0.05, 0.05)
[x1, x2] = np.meshgrid(X1, X2)
f = 100 * (x2 - x1 ** 2) ** 2 + (1 - x1) ** 2  # 给定的函数
plt.contour(x1, x2, f, 40)  # 画出函数的20条轮廓线

x0 = np.array([-1.2, 1])
out = dampnm(fun, gfun, hess, x0)
print("迭代次数:",out[2])
print("解：",out[0])

W = out[3]
print("迭代过程中点的变化：")
print(W[:, :])

plt.plot(W[0, :], W[1, :], 'g*-')
plt.show()
0 0.38147588128083515
1 4.950944723225031
2 3.757858643431574
3 0.4317760753882379
4 0.055964067473696845
5 9.624777931040847e-06
迭代次数: 5
解： [0.9999957  0.99999139]
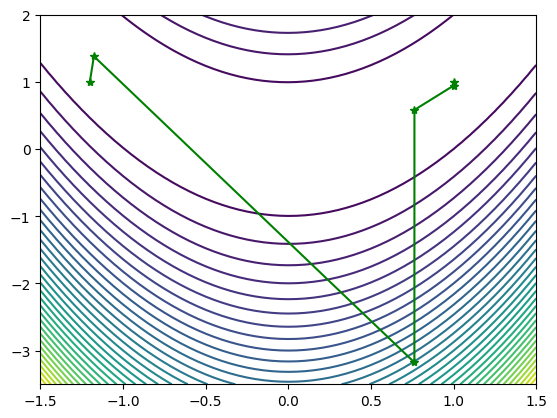
迭代过程中点的变化：
[[-1.2        -1.1752809   0.76311487  0.76342968  0.99999531  0.9999957 ]
 [ 1.          1.38067416 -3.17503385  0.58282478  0.94402732  0.99999139]]

png

实验结果

迭代次数和loss：

1
2
3
4
5
6
0   232.86768775422664
1   4.639426214066757
2   1370.789849446618
3   0.47311037910599685
4   25.027445596686427
5   8.60863341775635e-06

迭代第5次就跳出循环，可见牛顿法计算的非常快