数据分析方法概述

  1. 选模型（猜）
  2. 计算分析和证明（验）

拟合优度检验

可决系数

1710319675325

SSR占比列高说明拟合好

一元线性回归方程

拟合优度决定指标：R的平方（决定系数，可决系数）

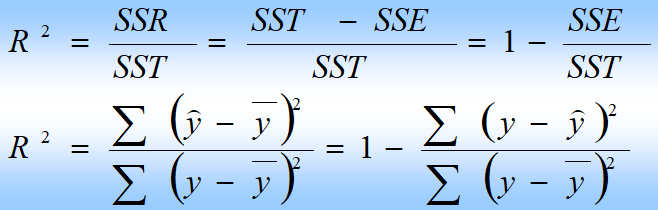
1710319875811

多元线性回归方程

adjust R

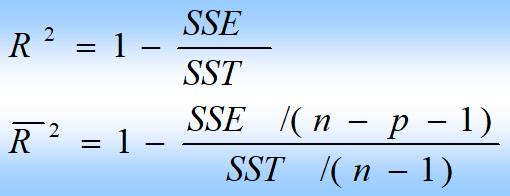
1710320098322

F检验

一元线性回归方程

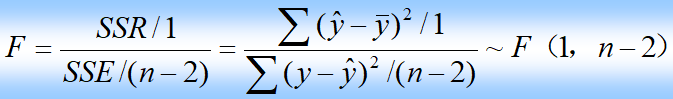
1710320763170

多元线性回归方程

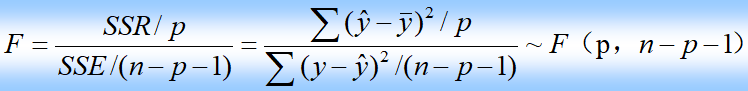
1710320796053

1710322416838

解释变量问题

引入解释变量多少个

①太少不能很好解释因变量的变化

②太多自变量间可能存在多重共线性

筛选策略

  1. 向前筛选（ Forward ）策略
  2. 向后筛选（ Backward ）策略

多重共线性

容忍度

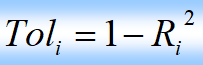
1710323184030

​ 取值范围在0-1之间，越接近0表示多重共线性越强

方差膨胀因子VIF

容忍度的倒数
VIF越大多重共线性越强，当VIF大于等于10时，说明存在严重的多重共线性。

特征根和方差比

①根据解释变量的相关系数矩阵求得的特征根中，如果最大的特征根远远大于其他特征根，则说明这些解释变量间具有相当多的重复信息。
②如果某个特征根既能够刻画某解释变量方差的较大部分比例（0.7以上），又能刻画另一解释变量方差的较大部分比例，则表明这两个解释变量间存在较强的线性相关关系。

条件指数

①指最大特征根与第i个特征根比的平方根。
②当条件指数在0-10之间时说明多重共线性较弱；
③当条件指数在10-100之间说明多重共线性较强；
④当条件指数大于100时说明存在严重的多重共线性

多重共线性的后果

（1）偏回归系数估计困难
（2）偏回归系数的估计方差随解释变量相关性的增大而增大
（3）偏回归系数的置信区间增大
（4）偏回归系数估计值不稳定性增大
（5）偏回归系数假设检验的结果不显著