信息论知识总结

引论

信息论的三个层次

基本信息论：山农信息论

一般信息论：通信的实际应用

广义信息论：各个领域

通信基本模型

信息指通信的数学理论

信息：消息中真正有用的

消息：信息的载体

通信三个基本要素：信源、信道、信宿

基本信息论

信息度量

信源的不肯定度

  • 信源的不肯定度表示为

    符合等概率时，不确定度最大；等概率时概率小，信息量大，长度可加。

自信息量

给定离散概率空间 $[X, P]$, 信源中某个具体消息的自信息量 $l(x)$ 定义为：
$l(x) = -log_{a}p(x)$ 其中 $x \in X$ .

  • 通信与信息中最常用的是以 2 为底，a = 2，单位为比特 (bit)；

  • 理论推导中以 e 为底较方便，a = e，单位为奈特 (Nat)；

  • 工程上以 10 为底较方便，a = 10，单位为笛特 (Det) 。

    可用对数换底公式进行单位互换：

    1 bit = 0.693 Nat = 0.301 Det。

  • 若 m 位二进制等长编码（码字），其提供的信息量为：

  • 若 m 位 D 进制等长编码（所有状态等概），其提供的信息量为：

    log 不写时，默认 a = 2，单位为 bit

熵

熵表示信源的不确定度，记为 H(X).

  • 熵的公式为：

  • 熵的特征：

    • 非负性
    • 连续性
    • 可加性
    • 等概率时，与取值空间的关系是单调递增的
    • 与发生概率 P 的关系是单调递减的

      熵在符合等概率时，不确定度最大；等概率时概率小，信息量大

联合熵和条件熵

联合熵

联合熵 (Joint Entropy) 度量的是一个二维随机变量 (X, Y) 的不确定度， 以$H(X, Y)$表示 。

  • 它表示同时观察 X 和 Y 所需的平均信息量。
  • 公式为：其中，$p(x, y)$ 是 X 和 Y 的联合概率分布。

条件熵

条件熵 (Conditional Entropy) 度量的是在已知随机变量 Y 的条件下，随机变量 X 的不确定度，以$H(X|Y)$表示。

  • 它表示在已知 Y 的情况下，描述 X 所需的平均信息量。

  • 公式为：

    其中，$p(x|y)$ 是在给定 $Y=y$ 时，$X=x$ 的条件概率。

互信息

互信息 $I(X; Y)$ 度量的是一个随机变量包含的关于另一个随机变量的信息量，或者说是一个随机变量的不确定性由于已知另一个随机变量而减少的量。

  • 互信息 $I(X; Y)$ 可以用熵和条件熵来表示：

  • 互信息 $I(X; Y)$ 具有以下性质：

    • 非负性：
    • 对称性：

熵函数

熵函数用于衡量随机变量的不确定性或信息量。

  • 定义：

    • 熵 H(X) 可以表示为 $H(X) = E(-(x)) = -\sum p(x)\log p(x)$。

  • 性质：

    • 对称性：熵函数的分量次序改变不影响其值。
    • 非负性：熵值大于等于 0 ($H(P) \geq 0$)。
    • 拓展性：小概率事件通常可以忽略，不影响熵的值。
    • 确定性：对于确定事件，熵值为 0 ，例如：$H_2(1, 0) = H_3(1, 0, 0) = … = H_n(1, 0, …, 0) = 0$。
    • 可加性：熵具有可加性，这与联合熵和条件熵有关。
    • 极值性：熵存在最大值，当所有事件等概率发生时，熵达到最大值 $H_n(p_1, p_2, …, p_n) \leq H_n(1/n, 1/n, …, 1/n) = \log n$。
    • 熵在等概率时，与取值空间的关系是单调递增的。

    • 熵与事件发生的概率 P 的关系是单调递减的。

      (错误):

      (错误):

      (正确):

微分熵

对于连续随机变量 X 且密度函数为 $p(x)$，定义 微分熵 为

微分熵 $h(X)$ 不一定为非负，不能直接与离散熵作绝对比较，仅作相对不确定度的度量。

消息冗余度

又称消息剩余度，信源实际熵与其最大可能熵之间的“空余”信息比例，反映了信源中可去除的多余信息。

  • 绝对冗余：

    • 离散信源：$H_{\max} = \log n$
    • 连续信源（微分熵）：取相应的 $h_{\max}$

  • 相对冗余：

    • $0 \le r \le 1$。
    • $r=0$ 时信源熵达到最大，无冗余；
    • $r=1$时无信息（极端冗余）。

  • 冗余度的意义：

    • 可压缩性：$r$越大，说明信源中可去除的冗余越多，压缩潜力越大。

    • 编码效率：实际平均码长 $L$ 与熵比值 $L/H$ 越接近 1，说明冗余度越低，编码越接近香农极限。

    • 设计参考：在信源编码时，可利用冗余度估算最佳压缩比。

连续信源的最大熵

1. 输出幅度受限

连续信源
  • 若 $a \le x \le b$，且概率密度函数 $p(x) = \frac{1}{b-a}$，则熵 $H(X) = \log(b-a)$。
  • 幅度受限时，均匀分布对应的熵最大。由于微分熵达到最大：
离散信源
  • 熵 $H(X) = - \sum p(x) \log p(x)$
  • 当等概率分布 $p(x) = \frac{1}{n}$ 时，熵最大 $H_{max}(X) = \log n$，其中 $n$ 为状态数。

2.输出平均功率受限

  • 熵 $H(X) = - \int_{-\infty}^{+\infty} p(x) \log p(x) dx$

  • 约束条件：

    • $\int_{-\infty}^{+\infty} p(x) dx = 1$ (概率密度函数归一化)
    • $\int_{-\infty}^{+\infty} x^2 p(x) dx = \sigma^2$ (平均功率为 $\sigma^2$)

  • 求解过程（利用拉格朗日乘子法）：

    • 构造函数 $F(x, p) = -p(x) \log p(x)$

    • $\frac{\partial F}{\partial p} = -[1 + \log p(x)]$

    • 利用变分法（拉格朗日乘子）构造泛函：

    • 变分条件 $\delta\mathcal{L}/\delta p = 0$ 给出，得到 $-(1 + \log p(x)) + \lambda_1 + \lambda_2 x^2 = 0$

    • 解得概率密度函数 $p(x) = e^{\lambda_1 - 1 + \lambda_2 x^2}$

    • 为了满足归一化条件和功率约束，可以证明 $\lambda_2 < 0$，令 $\lambda_2 = -\frac{1}{2\sigma^2}$，$\lambda_1 - 1 = \log \frac{1}{\sqrt{2\pi\sigma^2}}$

    • 最终得到 $p(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{x^2}{2\sigma^2}}$ (高斯分布)

  • 结论： 在平均功率受限的情况下，高斯分布对应的熵最大。

  • 最大熵为 。

，

，

，
由 得 ，
由 ，
联立以上两式可解得 和 。

信道容量

对于离散无记忆信道，输入符号 $X$ 的字母表$\mathcal{X}$，输出符号 $Y$ 的字母表 $\mathcal{Y}$，信道由条件概率 $P_{Y|X}(y|x)$ 描述。

典型容量公式：

  • 二元对称离散无记忆信道BSC： $C = 1 - H_2(p)$
  • 二元擦除离散无记忆信道BEC： $C = 1 - \varepsilon$
  • 连续带噪声信道AWGN： $C = \tfrac12\log(1 + P/\sigma^2)$

香农信道编码定理：

  • 对于任意离散记忆无信道，当码长 $n\to\infty$：

    • 若信息速率 $R < C$，存在一族编码/译码方案，使错误概率 $P_e\to0$；
      若 $R > C$，则任何编码方案的 $P_e$ 有界远离 0。
  • $C$ 是可实现的最大可靠通信速率。

基本编码理论定义与规则

基本定义

  • 码符号（Code Symbol）：构成码字的基本单位，常为二元 0/1。

  • 码字（Codeword）：由一个或多个码符号组成的序列，用于表示信源符号。

  • 码（Code）：信源符号到码字的映射集合。

  • D元码（Binary Code）：由A的元素构成，A有D种元素。

    二元码为符号集合为 {0,1} 的码，即D = 2(0,1)时。

  • 码长（Codeword Length）：一个码字中包含的码符号数量。

  • 信息位 (Information Bits, k) ：原始信息中包含的比特数量。

  • 码率 (Code Rate, η) ：信息位在码字中所占的比例，η = k/n。

    码率越高，传输效率越高，但影响纠检错，抗干扰能力可能下降。

  • 信道容量 (Channel Capacity) ：信道能够可靠传输信息的最大速率。

常见编码类型

  • 等长码（Fixed-Length Code）
    所有码字长度相等。
    优点：编码简单，便于同步。
    缺点：可能效率较低。

  • 非等长码（Variable-Length Code）
    码字长度可变。
    优点：可提高编码效率。
    缺点：需满足唯一可译性。

  • 单义码（Uniquely Decodable Code）
    任意码字串都能唯一分解为合法码字序列。

    单义$\Leftrightarrow\sum_{i=1}^{m}D^{-n_i}\le1$

  • 非续长码（Prefix Code）
    任一码字不是其他码字的前缀，又称前缀码。
    实现方式简单，适用于实时译码。

    非续长$\Rightarrow$单义，单义$\nRightarrow$非续长

  • 同价码（Equivalent Code）
    不同编码方案，码长分布和平均码长相同，即编码效率一致。

  • 瞬时码（Instantaneous Code）
    接收码字立即可译，无需后续码字辅助。前缀码是瞬时码的典型代表。

编码效率

设平均码长为 ( $\bar{L}$ )，信源熵为 ( $H(X)$ )，则：

树图

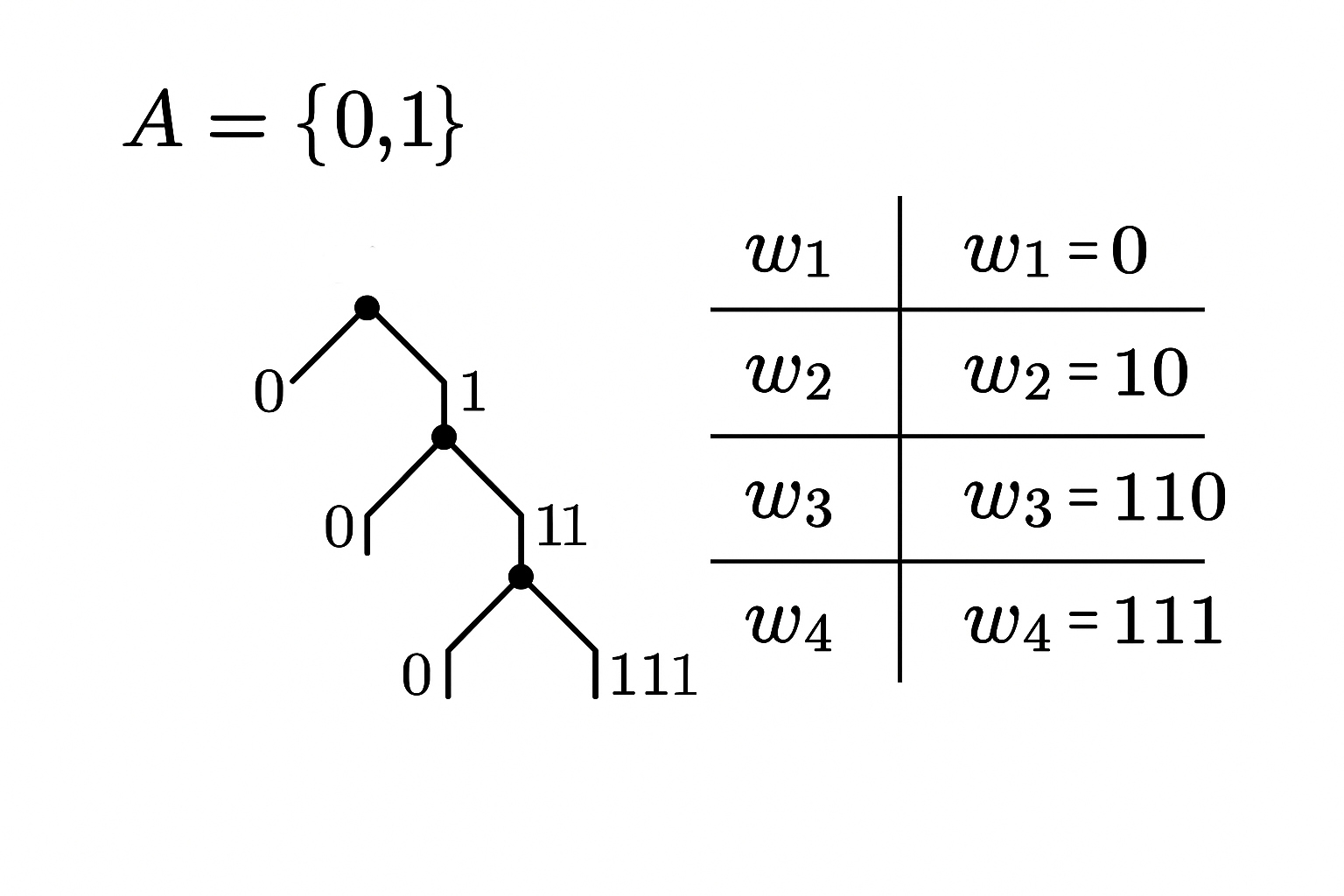
已生成图片

最佳效率编码

概述

在无损数据压缩中，最佳效率编码旨在将高概率符号映射到较短码字、低概率符号映射到较长码字，从而使平均码长接近信源熵。

香农–范诺编码

步骤

  1. 按符号出现概率从大到小排序。
  2. 将序列划分为两个概率总和尽量相等的子集，左分支标记“0”，右分支标记“1”。
  3. 对每个子集递归执行上述划分，直到每个符号成为叶节点。

复杂度

  • 排序 ($O(n\log n)$)，递归划分近似 ($O(n)$)，整体 ($O(n\log n)$)。

哈夫曼编码

步骤

  1. 将每个符号视为一棵树，权重为符号概率。
  2. 从森林中取出两个最小权重树，合并为新树，其权重为二者之和，标记左“0”右“1”。
  3. 重复直至只剩一棵树，根到叶子的路径即为各符号的码字。

复杂度

  • 使用优先队列合并，时间复杂度 ($O(n\log n)$)。

比较与应用

两者均为前缀码，保证唯一可译性。

特性 香农–范诺编码（Shannon–Fano Coding） 哈夫曼编码（Huffman Coding）
平均码长最优 否 是
构造复杂度 $O(n\log n)$ $O(n\log n)$
译码延迟 瞬时 瞬时
应用场景 简易压缩方案 通用压缩（ZIP、PNG）
基本思想 自上而下递归分割符号集，按概率分组 自下而上构建二叉树，合并最小概率节点
最优性 非最优前缀码（可能因分割策略不同失效） 严格最优前缀码（具有最小平均码长）

实际中Huffman编码可通过改进的堆结构（如斐波那契堆）进一步优化，而Shannon-Fano已逐渐很少被使用。

抗干扰编码

核心概念

  • 监督位/校验位 (Redundancy Bits, r)： 为了实现检错和纠错而添加的额外比特，r = n - k。

  • 汉明距离 (Hamming Distance)： 两个码字之间对应位置上不同符号的个数，$d = \sum_{i=1}^{n} |x_i - x_i’|$。

  • 检错 (Error Detection)： 检测传输过程中是否发生了错误。

  • 纠错 (Error Correction)： 不仅检测到错误，还能恢复出原始信息。

  • 时序码与非时序码：

    • 非时序码 ($m=0$)：又称逻辑码，编码输出只与当前输入有关，没有记忆性，例如分组码。

    • 时序码 ($m>0$)：编码输出不仅与当前输入有关，还与之前的输入有关，具有记忆性，例如卷积码。

      $m$为关联长度

  • 最小汉明距离 (Minimum Hamming Distance, dmin)： 码集中任意两个不同码字之间汉明距离的最小值。$d_{min}$ 是衡量编码检错和纠错能力的重要参数。

    • 检错能力： 为了检测 e 个错误，需要 $d_{min}$ ≥ e + 1。
    • 纠错能力： 为了纠正 t 个错误，需要 $d_{min}$ ≥ 2t + 1。

    • 同时纠正 t 个错误并检测 e 个错误 (e > t): 需要 $d_{min}$ ≥ t + e + 1

      image-20250517010335288

定比码

长度为 $n$的码字中恰好有 $k$ 个“1”，其余为“0”，常用于消除直流分量或辅助检错。

  • 示例：

    • 五三码：$n=5,k=3$，可用码字数 $C_5^3 = 10$
    • 七三码：$n=7,k=3$，可用码字数 $C_7^3 = 35$

  • 许用码字数：

  • 禁用码字数：

  • 编码效率：

  • 漏检概率（以五三码为例）：

    • 若传输中出现 2 位或 4 位错误，有可能落入另一个合法码字：

      • 二位错：
      • 四位错：
  • 总漏检概率：

一致监督检错码

在信息位后附加一位校验位，使得编码后的码字中 “1” 的个数为奇数或偶数。又称一致监督校验码和奇偶校验码，是用于检错的分组码。

  • 校验方程：

    • 设信息位为 $x_1, x_2, …, x_k$，校验位为 $x_n$，则码字为 $x_1, x_2, …, x_k, x_n$，其中 $n = k+1$。
    • 偶一致监督满足：$\sum_{i=1}^{n} x_i \equiv 0 \pmod{2}$，即偶数个1。
    • 奇一致监督满足：$\sum_{i=1}^{n} x_i \equiv 1 \pmod{2}$，即奇数个1。

  • 检错能力：可以检测出奇数个错误。无法检测出偶数个错误。

  • 误码率 (理论分析)：

    • 假设信道误码率为 $P_e$，码长为 $n$。

      通常取单码元误码概率$P_e = 10^{-4}$

    • 接收端发生 $i$ 位错误的概率为 $C_n^i P_e^i (1-P_e)^{n-i}$。

    • 对于偶校验，发生奇数个错误时可以检测出来，发生偶数个错误时检测不出来。

    • 未检出错误概率 ($P_{undetected}$): 发生偶数个错误的概率（不包括零个错误）。

    • 检错后剩余误码率 ($P’_{e}$): 在未检出错误的情况下，认为传输正确，但实际发生了偶数个错误。近似等于未检出错误概率的一半。

  • 编码效率：$\eta = (n-1)/n$

自动请求重发系统

简称ARQ系统，接收端检测到错误时，请求发送端重新发送数据。

  • 工作条件：

    • 有反向通道
    • 发端有存储设备
    • 发端有重发设备控制

  • 常见类型：停等 ARQ、后退 N 帧 ARQ 和 选择重传 ARQ

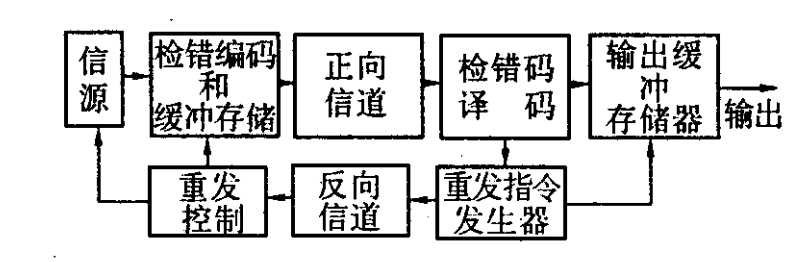
  • 工作示意图：image-20250516223614091

不适用于一站发多站收的同播工作模式

简易纠错码

简单重复码

  • 编码方式：将每个信息位重复发送多次。
  • 示例：信息位 “1” 编码为 “111”，信息位 “0” 编码为 “000” (重复 3 次)。
  • 编码效率：$\eta = 1/n$，若重复 $n$ 次。
  • 纠错能力：可以纠正 $\lfloor (n-1)/2 \rfloor$ 个错误。
  • 问题：效率太低

正反码

  • 编码方式：
    • 发送原始信息
    • 发送原始信息的反码
  • 编码效率：$\eta = 1/2$。
  • 码长：$k + k = 2k$ (示例 5+5=10)
  • 对 “1” 进行奇/偶一致监督
    • 奇数位为正码，示例：”11001” 编码为 “11001 11001”。
    • 偶数位为反码，示例：”10100” 编码为 “10100 01011”。
  • 纠错规则：“10110”为例
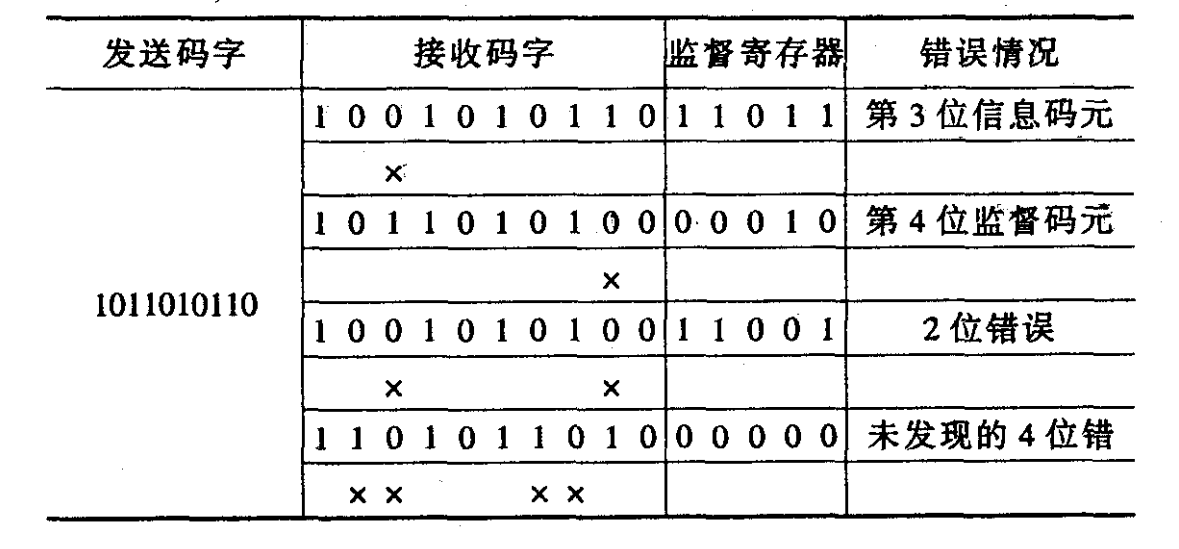
    image-20250516231536609

汉明码

一种可以纠正错误的线性分组码，称为 $(n, k)$ 码，$2^r \geq n+1$。

  • 参数： $(n, k)$ 汉明码的码长 $n$ 和n信息位长度 $k$ 满足 $n = 2^r - 1$，$k = n - r$，其中 $r$ 为校验位数。如(7, 4) 汉明码，$n=7, k=4, r=3$。

  • 监督矩阵 (H)：
    对于 $(n, k)$ 汉明码，监督矩阵$H$ 为 $(n-k) \times n$ 矩阵

  • 错误图样：，反映信道干扰和噪声对第$i$个码元的影响，收到码字的错误情况。

  • 校验矩阵 (S)：又称校验子，
    其中 是接收到的码组。

    • 如果 $S = 0$，则表示没有错误或发生了无法纠正的错误。
    • 如果 $S \neq 0$，对于可以纠正一位错误的汉明码，非零校验子直接指示了错误的位置（校验子对应的二进制数就是错误位的列号）。

    系统码指监督元在最后，反之为非系统码。

  • 生成矩阵 (G)：
    对于系统汉明码，，，即。

    G的每一行都是许用码字

  • $(7, 4)$ 汉明码：
    信息位 ，编码后的码字 ，其中 $G$ 是 的生成矩阵，$G = [I4 | Q{4 \times 3}]$。$H$ 是 的矩阵，，。

  • 编码效率： $\eta = k/n$

  • 误码率 ：$P \approx 1 - [(1-P_e)^n + nP_e(1-P_e)^{n-1}]$ (仅纠一位错)

卷积码

称为 码。表示每个时刻输入的比特数。表示每个时刻输出的比特数。$m$表示编码器的记忆长度，编码输出不仅与当前 个输入比特有关，还与前 $m$ 个时刻的输入比特有关。。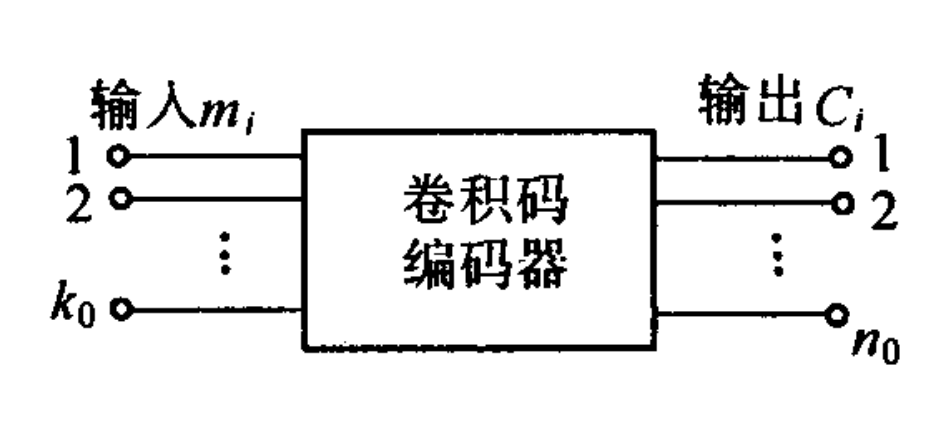image-20250517024922889

  • 编码器结构：通常由 $k_0$ 个输入移位寄存器和 $n_0$ 个模 2 加法器组成。每个移位寄存器的长度为 $m+1$。

  • 基本监督矩阵：

  • 一致监督矩阵：

    其中， () 为 阶矩阵，$0$ 为 阶全零矩阵， 为 阶单位矩阵。
    一致监督矩阵一共$m$块，

    • 校验位计算方式：

    • 一致监督矩阵： $h$向上向右推

  • 生成矩阵$G$：又称初始截短码生成矩阵，

    其中， 为 阶单位矩阵，$0$ 为 阶全零矩阵， () 为 阶矩阵 的转置矩阵。

  • 基本生成矩阵：

  • 初始截短码：一次性把列出$C_j$从第1个到第m个全列出。

    若输入信息组为 ，则输出的初始截断码组为：

信息论典型题目总结

求熵速率

题目1

一个信源以相等的概率及 1000 码元/秒的速率把“0”码和“1”码送入有噪声信道，由于信道中噪声的影响，发送为“0”接收为“1”的概率是 $1/16$，而发送为“1”接收为“0”的概率是 $1/32$， 求收信者接收的熵速率。

题1解

1. 确定信源的概率分布

2. 确定信道的转移概率

题中给出：

因此：

$Y=0$ $Y=1$
X=0 $15/16$ $1/16$
X=1 $1/32$ $31/32$

3. 计算联合概率分布 $P(X,Y)$

  • $X=0, Y=0$：
  • $X=0, Y=1$：
  • $X=1, Y=0$：
  • $X=1, Y=1$：
$Y=0$ $Y=1$
X=0 $15/32$ $1/32$
X=1 $1/64$ $31/64$

4. 计算接收信号的概率分布 $P(Y)$

$Y$ $P(Y)$
0 $31/64$
1 $33/64$

5. 计算接收信号的熵 $H(Y)$

数值计算（近似）：

6. 计算接收的熵速率 $R_y$

答：接收者的熵速率约为 1002.8 bits/秒。

题目2

有一个传输“0”“1”的二元数字通信系统，以 1000 码元/秒的速率传输，
发送“0”和“1”的概率分别为：

由于信道有噪声，误码率为

试求接收的信息速率。

题2解

1. 理解误码率

误码率 $P_e$ 是指发送的码元与接收的码元不一致的概率。
对于二元信道，错误可能为：

  • 发送 “0” 接收 “1”
  • 发送 “1” 接收 “0”

我们在这里做了一个假设，即发送 “0” 和 “1” 的误码率相同。

2. 确定转移概率

在简化假设下，无论发送 “0” 还是 “1”，发生错误的概率均为 $P_e$。

因此正确接收的概率：

$Y=0$ $Y=1$
X=0 0.998 0.002
X=1 0.002 0.998

3. 计算联合概率分布 $P(X,Y)$

  • $X=0, Y=0$：
  • $X=0, Y=1$：
  • $X=1, Y=0$：
  • $X=1, Y=1$：
$Y=0$ $Y=1$
X=0 0.3327 0.0007
X=1 0.0013 0.6653

4. 计算接收信号的概率分布 $P(Y)$

$Y$ $P(Y)$
0 0.3340
1 0.6660

5. 计算接收信号的熵 $H(Y)$

数值计算（近似）：

6. 计算接收的熵速率 $R_y$

答：接收的信息速率约为 919.1 bits/秒。

最大熵

题目

信源变量 $x$ 的取值为正，其平均值为 $A$，试求在信源熵最大的条件下的概率密度函数 $p(x)$ 以及最大熵 $H(x)$。

$p(x)$推导过程

1. 目标函数与约束条件

微分熵：

约束条件：

  • 归一化：$\int_0^\infty p(x)\,dx = 1$
  • 平均值约束：$\int_0^\infty x\,p(x)\,dx = A$

2. 构造拉格朗日函数

引入拉格朗日乘子 $\alpha, \beta$，得：

3. 求解极值（变分法）

对 $p(x)$ 求变分导数：

其中 $C = e^{-1 - \alpha}$

4. 利用约束求 $C, \beta$

归一化：

平均值约束：

5. 最大熵概率密度函数

$H(X)$计算

代入熵公式：

利用积分结果：

  • $\int_0^\infty \frac{1}{A} e^{-x/A} dx = 1$
  • $\int_0^\infty x \cdot \frac{1}{A} e^{-x/A} dx = A$

计算得：

答案

  • 最大熵分布为指数分布：
  • 最大熵值为：

最佳效率编码

题目

设有 6 个消息，其出现概率分别为：$ P(A)=1/16$,$P(B)=1/16$,$P(C)=2/16$,$P(D)=3/16$,$P(E)=4/16$,$P(F)=5/16$ 将它们分别进行香农编码和霍夫曼编码，并比较编码效率。

概率表

符号 概率 十进制
A 0.0625
B 0.0625
C 0.125
D 0.1875
E 0.25
F 0.3125

信息熵计算

计算得：

哈夫曼编码

构造过程（自底向上合并）

  1. 合并 A (1/16) 和 B (1/16) → AB = 2/16
  2. 合并 AB (2/16) 和 C (2/16) → (C,AB) = 4/16
  3. 合并 D (3/16) 和 E (4/16) → DE = 7/16
  4. 合并 (C,AB) 和 F (5/16) → ((C,AB),F) = 9/16
  5. 合并 DE 和 ((C,AB),F) → 根结点 = 1

使用二叉树将结点链接起来，规定左0右1，左大右小，可以得到霍夫曼编码树的大致结构

1
2
3
4
5
6
7
8
9
10
11
             (1)
         /         \
    (9/16)         (7/16)
  [F,(C,BA)]        [DE] 
    /    \         /    \
F(5/16)  (4/16)  D(3/16)E(4/16)
         [C,BA]
        /    \
     C(2/16) BA(2/16)
             /   \
          B(1/16) A(1/16)

码字分配

符号 编码
A 0111
B 0110
C 010
D 11
E 10
F 00

平均码长

香农-范诺编码

构造过程（自顶向下分组）

排序：F(5/16), E(4/16), D(3/16), C(2/16), A(1/16), B(1/16)，每次分组尽量平均。

  1. 划分为左组 {F,E} 和右组 {D,C,A,B}
  2. 左组 F, E → 00, 01
  3. 右组 D | {C,A,B} → 10, 11*
  4. 子组 C | {A,B} → 110, 111*
  5. A, B → 1110, 1111
1
2
3
4
5
6
7
8
9
             (1.0)
         /           \
  [F,E] (0.5625)    [D,C,A,B] (0.4375)
    /     \           /            \
F(0.3125)  E(0.25)   D(0.1875)     [C,A,B](0.25)
                                   /       \
                             C(0.125)   [A,B](0.125)
                                         /    \
                                     A(0.0625) B(0.0625)

码字分配

符号 编码
F 00
E 01
D 10
C 110
A 1110
B 1111

平均码长

编码效率比较

熵为：

平均码长：

编码效率比：

霍夫曼与香农编码的平均码长相同，略大于理论熵值，说明编码效率接近最优（大约 99%）。

卷积码

题目

已知初始截短卷积码的监督矩阵为：

输入信息序列为：$1011010\ldots$

要求写出其初始截短卷积码序列。

编码思路

  • (3,1,4)码，即$n_0=3$，$k_0=1$，$m=4$。
  • 每一行对应一个输出码组（每组3位），每组的第1位为当前信息位，第2、3位为监督位。
  • 前四组用一致监督矩阵，后面完备了用基本监督矩阵。

编码步骤

1. $H$计算前四组

根据

得出。

故前四组卷积码序列为
111，001，101，101

2. $h$计算后三组

由，

即

得到

3. 逐行填入信息位

组号 信息位 监督位1 监督位2 输出码组
1 1 1 1 111
2 0 0 1 001
3 1 0 1 101
4 1 0 1 101
5 0 1 1 011
6 1 1 0 110
7 0 1 0 010

编码结果

将各组拼接，得到初始截短卷积码序列：

即前21位为：“111 001 101 101 011 110 010”