ADF检验（单位根检验）

根据 P 值（result[1]）判断

假设

H０: 非平稳

H１: 平稳

判断

如果 P 值 ≤ 0.05：则反对零假设（H₀）： 数据平稳，没有单位根。

如果 P 值 > 0.05：则支持零假设（H₀）： 数据非平稳，有单位根。

单位根的存在意味着序列是非平稳的，无法直接用于建模，需要进行差分或其他变换。

1
2
3
4
5
6
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv("../data/Turbine_Data.csv",
                 low_memory=False,
                 parse_dates=["Unnamed: 0"])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
data['DateTime'] = data['Unnamed: 0'] 
data.drop('Unnamed: 0', axis=1, inplace=True)
data['DateTime'] = pd.to_datetime(data['DateTime'], 
 format = '%Y-%m-%dT%H:%M:%SZ', 
 errors = 'coerce') # 如果在日期时间转换过程中遇到错误，将错误值转换为 NaT，处理不规则或无效日期时间数据
data['year'] = data['DateTime'].dt.year
data['month'] = data['DateTime'].dt.month
data['day'] = data['DateTime'].dt.day
data['hour'] = data['DateTime'].dt.hour
data['minute'] = data['DateTime'].dt.minute
data.drop('DateTime', axis=1, inplace= True)
for label, content in data.items():
    if pd.api.types.is_numeric_dtype(content): # 判断是否为数值型
        if pd.isnull(content).sum():
            data[label+"_is_missing"] = pd.isnull(content)
            data[label] = content.fillna(content.median())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from statsmodels.tsa.stattools import adfuller
test_result=adfuller(data['ActivePower'])

def adfuller_test(Power):
    result=adfuller(Power)
    labels = ['ADF Test Statistic','p-value','#Lags Used','Number of Observations Used']
    for value,label in zip(result,labels):
        print(label+' : '+str(value) )
    if result[1] <= 0.05:
        print("有证据反对零假设(H0),支持备择假设(H1)。没有单位根，是平稳的")
    else:
        print("没有证据反对零假设(H0),拒绝备择假设(H1),有单位根,是非平稳的 ")
        
adfuller_test(data['ActivePower'])
ADF Test Statistic : -21.001664058258655
p-value : 0.0
#Lags Used : 71
Number of Observations Used : 118152
有证据反对零假设(H0),支持备择假设(H1)。没有单位根，是平稳的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import pandas as pd
from pandas import Series
import numpy as np
import datetime
from pandas_datareader import data as pdr
import matplotlib.pyplot as plt
import seaborn
from prophet import Prophet
import statsmodels.api as sm
import statsmodels.tsa as ts
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.tsa.arima_model import ARIMAResults
from sklearn.neural_network import MLPRegressor
# from sklearn.metrics import scorer
from sklearn.metrics import accuracy_score
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
from matplotlib import pyplot
import itertools as it
from matplotlib import mlab
# import pmdarima as pm

确定ARIMA（p,d,q）模型参数

确定d

判断序列是否平稳：
p值 < 0.05：序列平稳，d=0。
p值 ≥ 0.05：序列非平稳，需要差分。
对非平稳序列使用 .diff() 函数进行一次差分，直到序列平稳，看需要差分的阶数。

确定AR和MA的阶数

通过分析 ACF（自相关函数） 和 PACF（偏自相关函数） 来选择p和q。

ACF 和 PACF 的作用

  • ACF 图：显示序列与其滞后值的相关性，帮助确定q（MA 部分的阶数）。
  • PACF 图：显示序列与其滞后值去除中间影响后的相关性，帮助确定p（AR 部分的阶数）。

    观察特征

  • PACF 图：
    截尾（某个滞后阶后骤减为 0）：对应 AR 模型的阶数p。
  • ACF 图：
    截尾：对应 MA 模型的阶数q。
    如果两个图均呈指数衰减或振荡，则可能需要混合模型（ARMA 或 ARIMA）。

    ACF：显示数据随时间滞后逐渐衰减的程度。对于非平稳数据，ACF 通常缓慢衰减；而平稳数据的 ACF 在一定滞后之后会迅速归零。

PACF：帮助识别数据的直接滞后相关性。例如，如果 PACF 在某个滞后阶数后迅速归零，说明可以用少量滞后项捕获数据的主要信息。

1
2
3
4
5
6
7
8
9
10
11
# 原始数据ACF和PACF图像
fig = plt.figure(figsize=(10,6))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data['ActivePower'], lags=30, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data['ActivePower'], lags=30, ax=ax2)
plt.xlabel('Time lag')
plt.show()
# ACF在滞后阶数 3 之前逐渐衰减，滞后 4 及以后衰减变慢并接近 0，说明 MA 部分的阶数 q 为 3
# 在滞后阶数为 1 和 2 处，PACF 显示显著的相关性，而其后的相关性较小，表明 AR 部分的阶数p为2

png
​ 

1
2
3
4
5
6
7
8
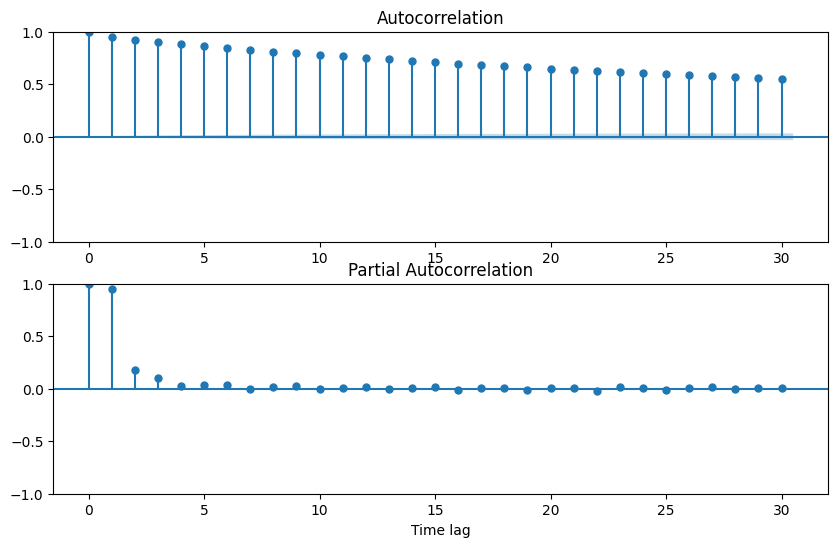
# # 差分后的ACF和PACF图像
# fig = plt.figure(figsize=(10,6))
# ax1 = fig.add_subplot(211)
# fig = sm.graphics.tsa.plot_acf(data['ActivePower'].diff().dropna(), lags=30, ax=ax1)
# ax2 = fig.add_subplot(212)
# fig = sm.graphics.tsa.plot_pacf(data['ActivePower'].diff().dropna(), lags=30, ax=ax2)
# plt.xlabel('Time lag')
# plt.show()
1
2
3
4
5
# 前 5000 个点作为样本
from statsmodels.tsa.arima.model import ARIMA
model=ARIMA(data['ActivePower'][:5000],order=(2,0,3))
model_fit=model.fit()
print(model_fit.summary())
                               SARIMAX Results                                
==============================================================================
Dep. Variable:            ActivePower   No. Observations:                 5000
Model:                 ARIMA(2, 0, 3)   Log Likelihood              -30684.066
Date:                Thu, 12 Dec 2024   AIC                          61382.131
Time:                        23:05:03   BIC                          61427.752
Sample:                             0   HQIC                         61398.121
                               - 5000                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const        368.0024     34.537     10.655      0.000     300.310     435.694
ar.L1          0.8269      0.175      4.716      0.000       0.483       1.171
ar.L2          0.1210      0.168      0.720      0.471      -0.208       0.450
ma.L1         -0.0759      0.176     -0.432      0.666      -0.420       0.268
ma.L2         -0.0235      0.037     -0.630      0.529      -0.097       0.050
ma.L3          0.0535      0.009      5.774      0.000       0.035       0.072
sigma2      1.255e+04     99.179    126.571      0.000    1.24e+04    1.27e+04
===================================================================================
Ljung-Box (L1) (Q):                   0.00   Jarque-Bera (JB):             62397.70
Prob(Q):                              1.00   Prob(JB):                         0.00
Heteroskedasticity (H):               0.58   Skew:                             0.72
Prob(H) (two-sided):                  0.00   Kurtosis:                        20.25
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

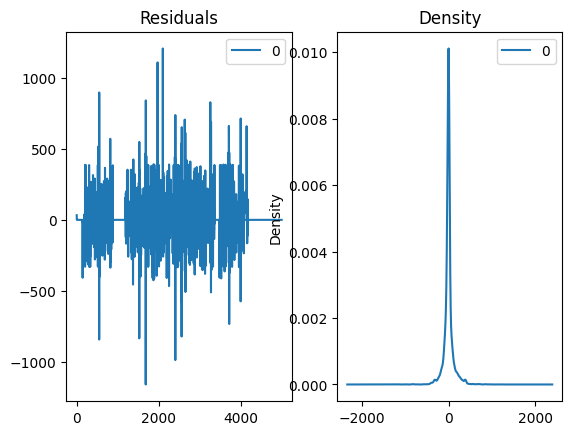
残差分析

残差是评价模型拟合效果的重要依据。理想情况下，残差应该是白噪声（独立同分布的随机变量，均值为 0）。

  • 残差图：检查残差是否随机分布。检查残差的分布是否无偏且无明显趋势。如果残差存在明显的趋势或周期性，说明模型拟合不足。
  • 残差密度图：检查残差分布是否接近正态分布。如果分布偏离正态分布，可能表明模型未捕获某些特征。
1
2
3
4
5
6
7
residuals = pd.DataFrame(model_fit.resid)
# 在 ax[0] 中绘制残差随时间变化的残差图
fig, ax = plt.subplots(1,2)
residuals.plot(title="Residuals", ax=ax[0])
# 在 ax[1] 中绘制残差的概率密度分布（核密度估计，KDE）
residuals.plot(kind='kde', title='Density', ax=ax[1])
plt.show()

​
png
​ 

1
2
3
4
5
6
7
8
9
10
# 将生成预测值与原始数据的对比图。这有助于直观地查看模型的拟合效果以及预测的准确性。预测未来100个时间点
forecast = model_fit.forecast(steps=100) 
plt.figure(figsize=(10, 6))
plt.plot(range(5000, 5100), forecast, label='Forecast', color='red') # 预测数据
plt.plot(data['ActivePower'][:5000], label='Training Data') # 训练数据
plt.title("ARIMA Model Predictions")
plt.xlabel("Time")
plt.ylabel("Active Power")
plt.legend()
plt.show()

​
png
​ 

1
2
3
4
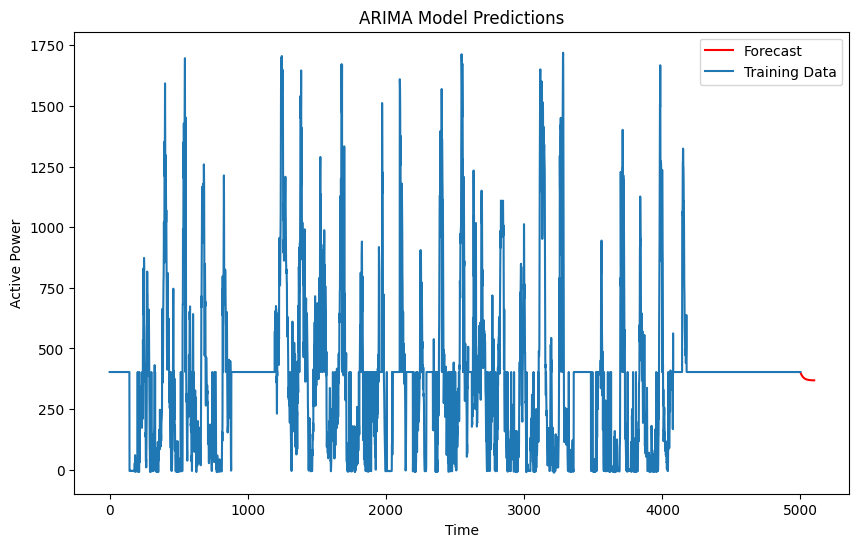
# 划分训练集和测试集
from sklearn.model_selection import train_test_split
train = data['ActivePower'][:1000]
test = data['ActivePower'][1000:1015]
1
2
3
4
5
6
7
8
9
# 获取预测结果及置信区间
forecast_result = model_fit.get_forecast(steps=15)
fc = forecast_result.predicted_mean
conf = forecast_result.conf_int(alpha=0.05)

# 转换为 Pandas Series
fc_series = pd.Series(fc, index=test.index)
lower_series = pd.Series(conf.iloc[:, 0], index=test.index)
upper_series = pd.Series(conf.iloc[:, 1], index=test.index)

各个误差指标的计算方法：

MAPE (Mean Absolute Percentage Error)：

  • 公式：MAPE = np.mean(np.abs(forecast - actual) / np.abs(actual))
  • 用于衡量预测值与实际值之间的百分比误差，值越小越好。

ME (Mean Error)：

  • 公式：ME = np.mean(forecast - actual)
  • 计算预测误差的均值，用于衡量预测的偏差。

MAE (Mean Absolute Error)：

  • 公式：MAE = np.mean(np.abs(forecast - actual))
  • 衡量预测误差的绝对值的平均，越小越好。

MPE (Mean Percentage Error)：

  • 公式：MPE = np.mean((forecast - actual) / actual)
  • 衡量预测误差的百分比，注意，MPE 可能出现正负偏差。

RMSE (Root Mean Square Error)：

  • 公式：RMSE = np.sqrt(np.mean((forecast - actual)**2))
  • 衡量预测误差的标准差，越小越好。

Correlation Coefficient (corr)：

  • 公式：corr = np.corrcoef(forecast, actual)[0, 1]
  • 计算预测值与实际值之间的相关系数，值范围在 -1 到 1 之间，越接近 1 说明预测越准确。

MinMax：

  • 公式：minmax = 1 - np.mean(mins / maxs)
  • 衡量预测值与实际值之间的最小-最大误差。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def forecast_accuracy(forecast, actual):
    forecast = np.array(forecast)
    actual = np.array(actual)

    # 指标计算
    mape = np.mean(np.abs(forecast - actual) / np.abs(actual))  # MAPE
    me = np.mean(forecast - actual)  # ME
    mae = np.mean(np.abs(forecast - actual))  # MAE
    mpe = np.mean((forecast - actual) / actual)  # MPE
    rmse = np.mean((forecast - actual)**2)**0.5  # RMSE
    corr = np.corrcoef(forecast, actual)[0, 1]  # Correlation
    mins = np.amin(np.column_stack((forecast, actual)), axis=1)
    maxs = np.amax(np.column_stack((forecast, actual)), axis=1)
    minmax = 1 - np.mean(mins / maxs)
    return {'mape': mape, 'me': me, 'mae': mae, 'mpe': mpe, 'rmse': rmse, 'corr': corr, 'minmax': minmax}
forecast_accuracy(fc, test.values)
{'mape': np.float64(0.026126326051675634),
 'me': np.float64(-10.519893029273199),
 'mae': np.float64(10.519893029273199),
 'mpe': np.float64(-0.026126326051675634),
 'rmse': np.float64(11.600579744847185),
 'corr': np.float64(-1.5501431965421824e-15),
 'minmax': np.float64(0.02612632605167564)}