建立离散传递函数

T1

题目

程序

T = 1;
num1 = [5 2];
num2 = [17 10.7 3.2 0 0 0];
den1 = [1 -0.3 -0.5 0.06];
den2 = [-300 82.2 112.1 158 -7.3 1];
% 求零极点和增益
[z1, p1, k1] = tf2zp(num1, den1);
[z2, p2, k2] = tf2zp(num2, den2);
% 零极点离散模型
Gz1 = tf(num1, den1, T) 
Gz2 = tf(num2, den2, T)
% 单位闭环传函
sys1 = feedback(Gz1,1); 
sys2 = feedback(Gz2,1);
% 在复平面上绘制零极点图
figure;
    % 绘制 Gz1 的零极点图
subplot(2, 1, 1); % 创建一个 2 行 1 列的子图，并将当前子图设置为第 1 个
pzmap(Gz1);
title('Gz1 零极点图');
    % 绘制 Gz2 的零极点图
subplot(2, 1, 2); % 创建一个 2 行 1 列的子图，并将当前子图设置为第 2 个
pzmap(Gz2);
title('Gz2 零极点图');
% 分析系统稳定性
isStable(sys1, 'Gz1表示的系统')
isStable(sys2, 'Gz2表示的系统')
function isStable(sys, sysName)
    p = pole(sys);
    if all(real(p) < 0)
        disp([sysName '是稳定的，所有极点都在复平面的左半部']);
    else
        disp([sysName '是不稳定的，因为一个或多个极点位于复平面的右半部分']);
    end
end

结果

1. 零极点图
   
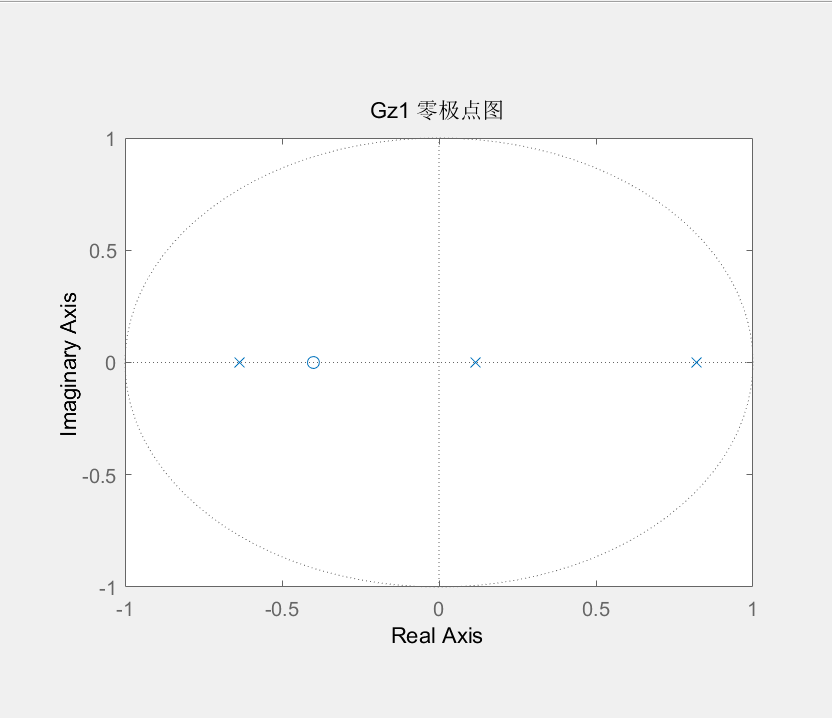
2. 判断稳定性

Gz1表示的系统是不稳定的，因为一个或多个极点位于复平面的右半部分
Gz2表示的系统是不稳定的，因为一个或多个极点位于复平面的右半部分

T2

T3

题目

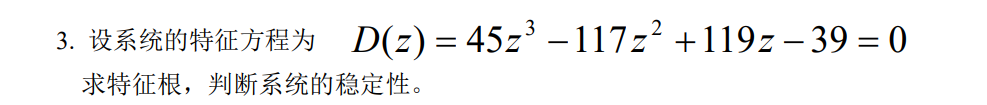
程序

syms z ; 
D = 45 * z^3 - 117 * z^2 + 119 * z^1 - 40 
% 特征多项式
G = sym2poly(D);
% 解特征根
r = roots(G) 
% 判断系统是否稳定
isStable(r)
function isStable(r)
    if all(real(r) < 0)
        disp(['该系统是稳定的，所有特征根都在复平面的左半部']);
    else
        disp(['该系统是不稳定的，因为一个或多个特征根位于复平面的右半部分']);
    end
end

结果

1. 特征根

   r =

   0.9807 + 0.6558i
   0.9807 - 0.6558i
   0.6386 + 0.0000i

2. 判断稳定性

   该系统是不稳定的，因为一个或多个特征根位于复平面的右半部分

T4

题目

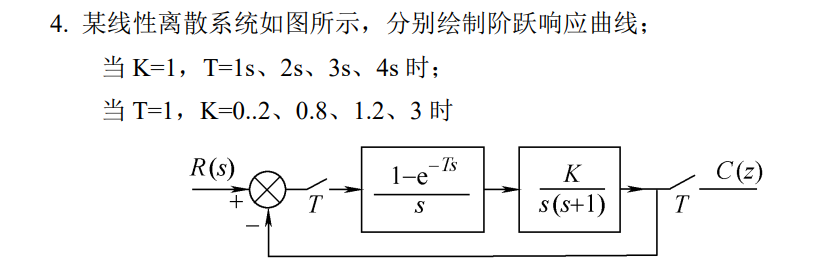
程序

% 当 K=1，T=1s、2s、3s时的阶跃响应
for(i=1:1:3)
    StepResponse(1, i);
end
% 当 T=1s，K=0.2、0.8、1.2、3时的阶跃响应
StepResponse(0.2, 1);
StepResponse(0.8, 1);
StepResponse(1.2, 1);
StepResponse(3, 1);
% 求解离散系统的单位阶跃响应
function StepResponse(K, T)
num = [K];
den = [1 1 0];
G = tf(num, den)
Gz =c2d(G, T, 'zoh') % 零阶保持器法离散化
Fai = feedback(Gz, 1, -1) % 离散函数单位负反馈
figure;
step(Fai) % 绘制离散和连续函数阶跃响应
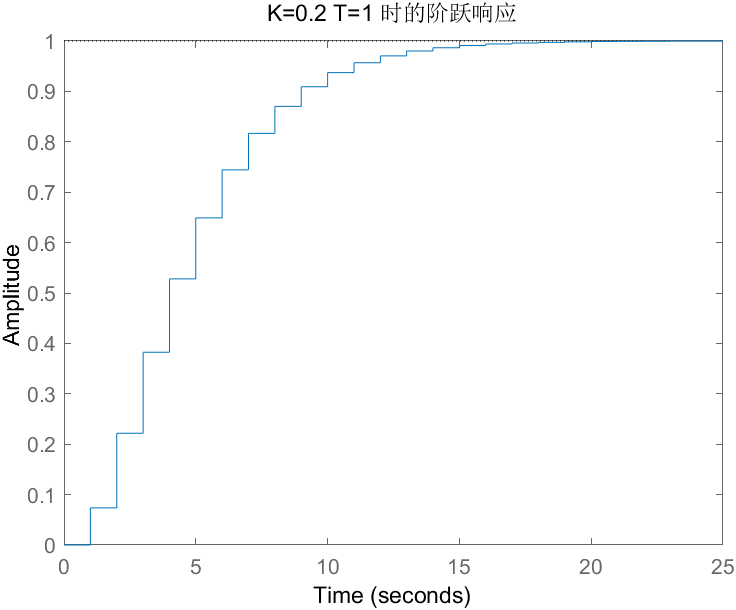
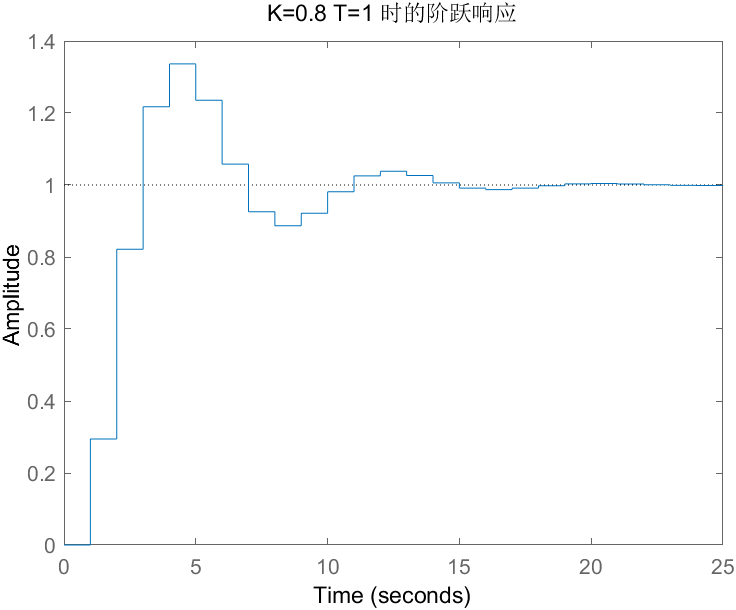
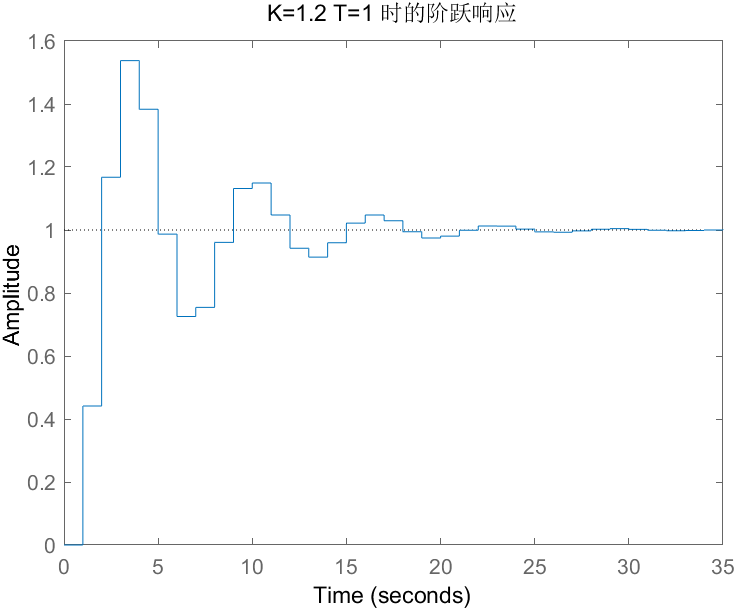
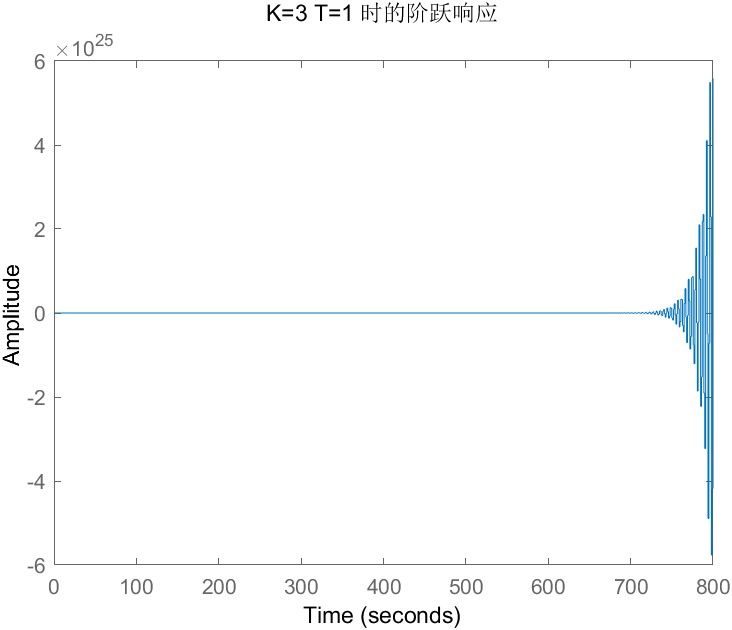
title(['K=', num2str(K), ' T=', num2str(T), ' 时的阶跃响应']);
end

结果

1. 当 K=1，T=1s、2s、3 s时
   
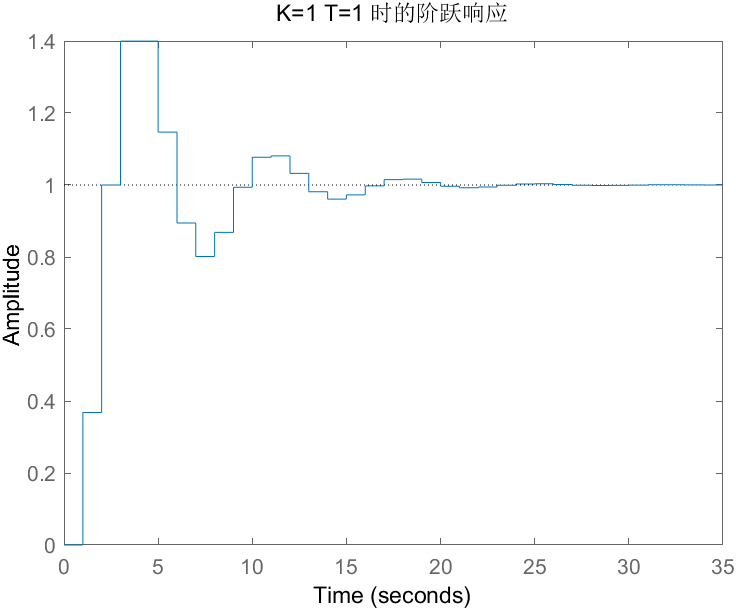
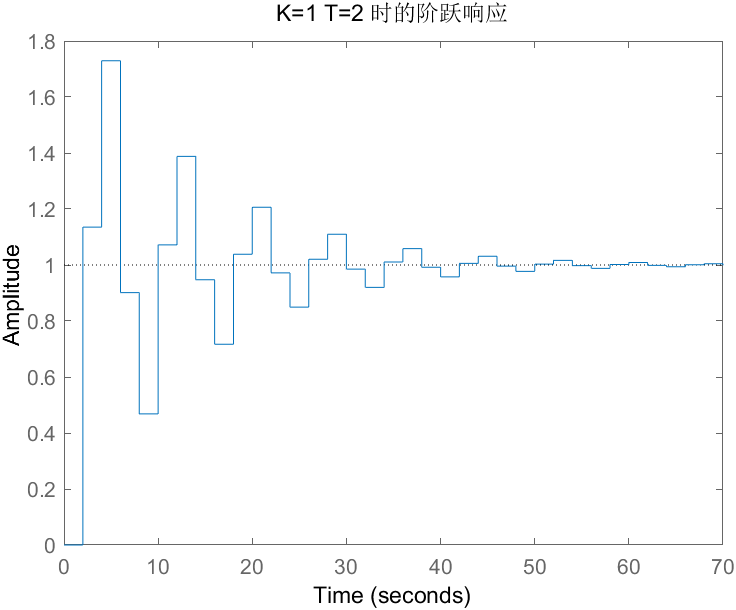
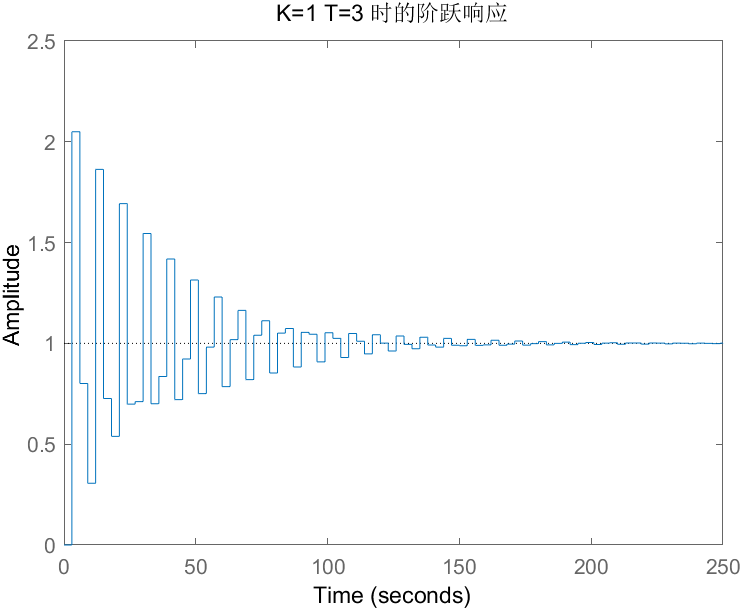
2. 当 T=1s，K=0.2、0.8、1.2、3时