离散控制系统
离散控制系统
T1
题目

程序
1 | % 定义模拟调节器的传递函数 |
结果
- 脉冲传递函数 D(z)
1 | Dz = |
差分方程的输出曲线和D(z)的输出曲线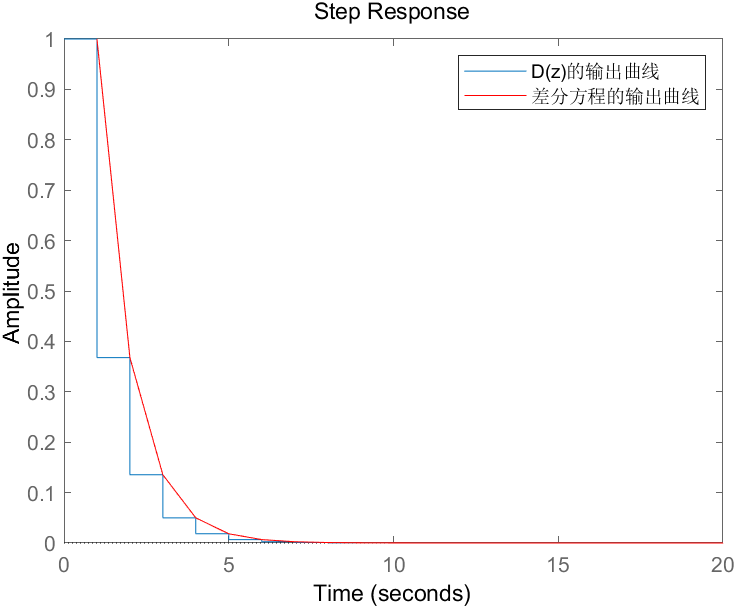
T2
题目
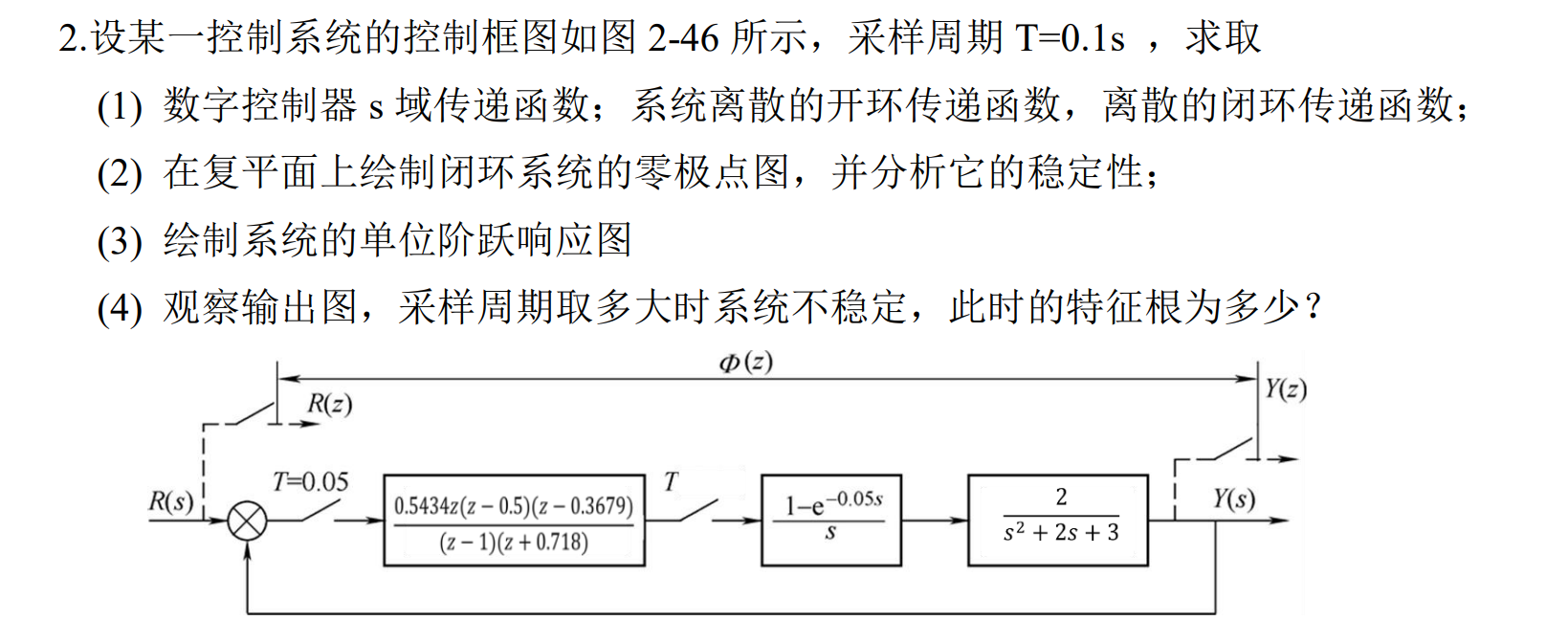
代码
1 | z = [0.5, 0.3679]; |
结果
数字控制器 s 域传递函数;系统离散的开环传递函数,离散的闭环传递函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35D =
0.5434 (z-0.5) (z-0.3679)
-------------------------
(z-1) (z+0.718)
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.
Gz =
0.002417 z + 0.002338
----------------------
z^2 - 1.898 z + 0.9048
Sample time: 0.05 seconds
Discrete-time transfer function.
openz =
0.0013135 (z-0.5) (z-0.3679) (z+0.9672)
---------------------------------------
(z-1) (z+0.718) (z^2 - 1.898z + 0.9048)
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.
Faz =
0.0013135 (z-0.5) (z-0.3679) (z+0.9672)
---------------------------------------------
(z+0.7179) (z-0.9274) (z^2 - 1.969z + 0.9755)
- 闭环系统的零极点图及稳定性分析
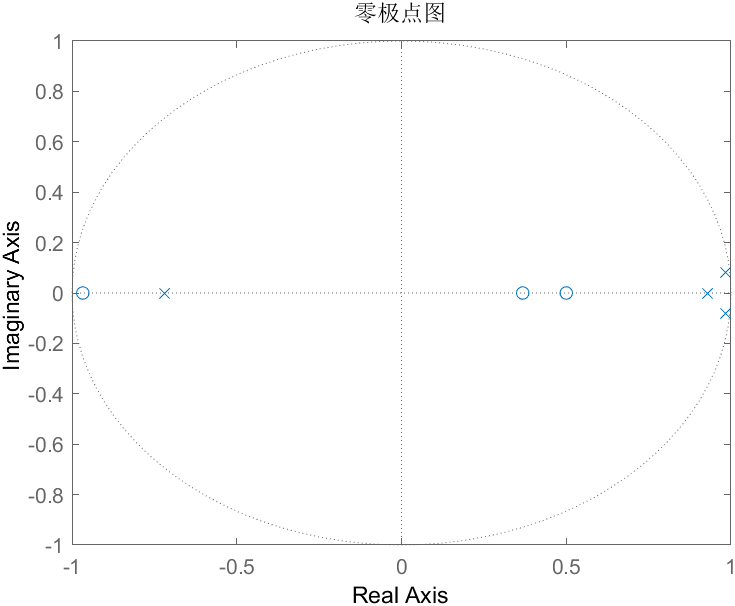
系统是不稳定的,因为一个或多个极点位于复平面的右半部分
系统的单位阶跃响应图
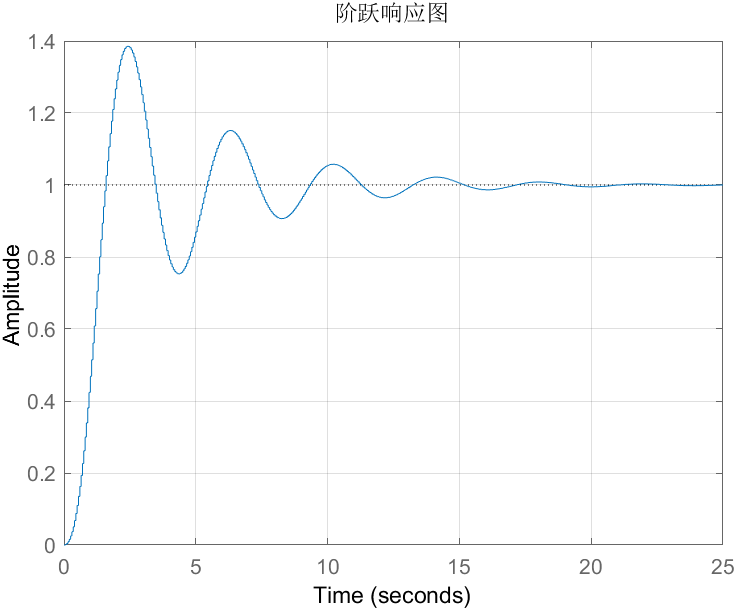
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 thewindsing!
评论