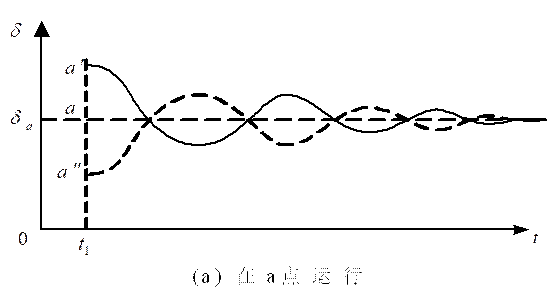电力系统稳定性分析

摘要

本文主要对电力系统的稳定性分析进行了总结与探讨。电力系统的稳定性是指在扰动后系统能够继续稳定运行的能力，分为频率稳定、电压稳定和同步稳定三种类型。本文首先介绍了动态模型分析，重点阐述了同步发电机组在扰动下的运动方程，并分析了励磁调节对系统稳定性的影响。接着，讨论了静态稳定性，包括小扰动下系统恢复能力的分析方法，并通过代数判据（如胡尔维茨判据）进行了定量分析。文章还提出了提高静态稳定性的若干措施，如减小发电机电抗、线路电抗等。最后，本文对暂态稳定性进行了分析，强调了“等面积法则”在系统恢复中的作用，并提出了增强暂态稳定性的措施，如故障快速切除、自动重合闸等。整体而言，本文对电力系统的稳定性分析方法、提升稳定性的措施提供了系统性总结，并为实际电力系统的稳定性评估与优化提供了理论依据。

关键词：电力系统稳定性分析；动态模型；静态模型；定量分析；暂态稳定性；提高稳定性措施

---

1. 电力系统稳定性分析的动态模型

1.1 电力系统稳定性定义

电力系统稳定性：指电力系统受到一定的扰动后能否继续运行的能力。

• 频率稳定：指电力系统受到一定的扰动后，系统频率能否保持在允许范围内的能力。
• 电压稳定：指电力系统受到一定的扰动后，各节点电压能否继续保持在允许范围内的能力。
• 同步稳定（功角稳定）：指电力系统受到一定的扰动后，各发电机组能否继续保持同步运行的能力。

---

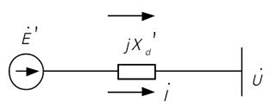
同步发电机组运动方程

同步发电机运动时如下图

忽略转子损耗时，运动方程为：

$$J\frac{d^2\beta}{dt^2} = M_s$$

其中：

• $M_s = M_m - M_0$（机械转矩与电磁转矩差）
• $\beta$ 为转子角位移

电量对时间求导得：

$$\frac{d\bar{\sigma}}{dt} = \omega - \omega_N$$ $$\frac{d^2\bar{\sigma}}{dt^2} = \frac{d\omega}{dt}$$

最终得到标幺值方程：

$$\tau_J\frac{d^2\sigma}{dt^2} = P_a$$

---

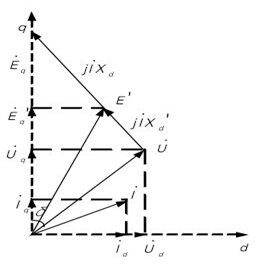
1.2电力系统稳定性分析的静态模型

当励磁不调节时（$E_q$恒定），系统静态特性由以下方程描述：

$$\begin{cases} U = U_d + jU_q \\ I = I_d + jI_q \\ E_q = U + jI X_d \end{cases}$$

展开得：

$$\begin{cases} E_q = U_q + I_d X_d \\ 0 = U_d - I_q X_d \end{cases}$$

功率方程为：

$$\begin{cases} P_{Eq} = U_q I_q + U_d I_d \\ Q_{Eq} = U_q I_d - U_d I_q \end{cases}$$

代入$U_d = U \sin\delta$、$U_q = U \cos\delta$，得到功角特性：

$$P_{Eq} = \frac{E_q U}{X_d} \sin\delta$$ $$Q_{Eq} = \frac{E_q U}{X_d} \cos\delta - \frac{U^2}{X_d}$$

有功功率和无功功率的功角特性：

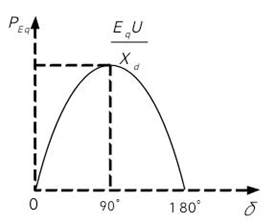
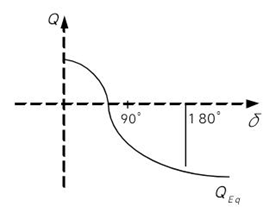
当励磁调节时，则$E_q$会发生变化

有功功率功角特性

---

2. 电力系统静态稳定性分析

2.1 静态稳定判据

平衡点处功率特性曲线满足：

$$\frac{dP}{d\delta} > 0 \quad (\delta < 90^\circ)$$

• 稳定平衡点（如a点）：扰动后能恢复
• 不稳定平衡点（如b点）：扰动后失稳

2.2 小扰动法分析

线性化微分方程：

$$T_J\frac{d^2\Delta\delta}{dt^2} + \left(\frac{dP_{Eq}}{d\delta}\right)\Delta\delta = 0$$

电力系统静态稳定性的定量分析

电力系统静态稳定性：指电力系统受到小的扰动后，恢复稳定的能力

平衡点：不考虑损耗时，输入等于输出时的一种状态，即相当于合力等于零的状态。系统正常运行时， $P_m$（输入的机械功率）= $P_e$（输出的电磁功率），其中 Pm使转子加速， $P_e$使转子减速。即在下图中的$a$点和$b$点运行。

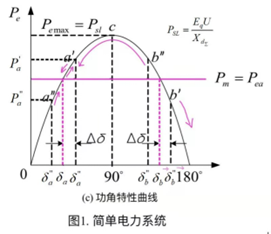
在a点收到扰动后：
​ ① 当系统受到小的干扰，引起功角 $δ$ 增加一个微量 $Δδ$ 时：$Pe$ 从 $P{eb}$ 变到 $P{eb1}$，$δ$ 也将从 $δ_b$ 变到 $δ{b1}$；由于 $Pm$ 恒定，即 $P_m > P{eb1}$，因此当这个扰动消失后，机组将减速，功率角将从 $δ{a1}$ 开始减小。当 $δ$ 从 $δ{a1}$ 减小到 $δ_a$ 时，虽然 $P_m = P_e$，但由于机械惯性的原因，$δ$ 将继续减小。当 $δ$ 小于 $δ_a$ 后，$P_m$ 将大于 $P_e$，机组又将加速，$δ$ 将又增大并通过 $a$ 点；如此循环下去。考虑到摩擦、风阻等损耗，$δ$ 将最终回到 $δ_a$ 的位置，重新达到稳定运行的状态。

​ ② 同样可以分析，当系统受到小的干扰，引起功角 $δ$ 减小一个微量 $Δδ$ 时，也将最终回到 $δ_a$ 的位置。

在有阻尼情况下功角随时间的变化如下图所示

​

在b点收到扰动后：

​ ① 当系统受到小的干扰，引起功角δ 增加一个微量Δδ时：Pe从 Peb变到 Peb ，δ也将从δb变到δb’；由于Pm 恒定，即Pm> Peb ，因此当这个扰动消失后，机组将加速，功率角δ 将增大；随着 δ的进一步增大，Pe将进一步减小，转子上的不平衡功率（即加速功率）将愈来愈大，使 更进一步增大。这样循环不已，功率角不断增大，运行点不再能回到b，系统失去稳定。功率角的不断增大，标志着两个发电机之间将失去同步，电力系统将瓦解。

​ ② 当系统受到小的干扰， 引起功率角δ 减小一个微量Δ δ 时：Pe从 Peb变到Peb” ， δ也将从δb 变到δb1”；由于Pm 恒定，即 Peb”>Pm。因此当这个扰动消失后，机组将减速，功率角 δ将减小； δ的减小将使电磁功率进一步增大，而 Pe的增大又使δ 进一步减小，至c点时，减速的加速度达到最大值； δ通过 δc=90后，将继续减小，但减速加速度将减小；如此变化下去，最终在a点达到新的平衡并稳定运行，但运行点不再回到b点。

在有阻尼情况下功角随时间的变化如下图所示，可观察到系统失稳。

​

对一、二两种情况的归纳：

功角特性曲线上，虽有两个对应于$P_m=P_e $的运行点$a$、$b$，但其中只有$a$点是可以稳定运行的运行点（称为“稳定的平衡点”）；而$b$点是不稳定的运行点（称为“不稳定的平衡点”）。

2.3 胡尔维茨判据

对特征方程：

$$a_0\lambda^n + a_1\lambda^{n-1} + \cdots + a_n = 0$$

• 必要条件：所有系数符号相同且$a_0 > 0$
• 充要条件：各阶胡尔维茨行列式均正

各阶胡尔维茨行列式：

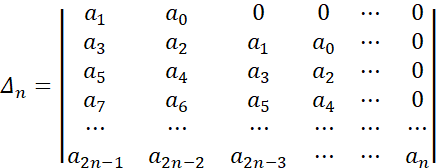
示例：二阶系统

$$\Delta_2 = \begin{vmatrix} a_1 & a_0 \\ a_3 & a_2 \end{vmatrix} > 0$$

2.4静态平衡和提高静态稳定性措施

由图可知，a点稳定平衡点， b点不稳定平衡点。

​

想要提高静态稳定性有以下措施：

1.减小发电机的电抗

（1）减小变压器的电抗

（2）减小线路电抗：

2.采用分裂导线：

3.单回线变双回线：

4.采用串联电容器补偿：

（1）改善系统的结构

（2）采用自动控制装置（如励磁控制等）

---

3. 暂态稳定性分析

3.1 等面积法则

系统维持暂态稳定的条件：

$$\text{减速面积} = \text{加速面积}$$

能量分析：

• 加速面积：$ W1 = \int{\delta_0}^{\delta_c} P_m d\delta $
• 减速面积：$ W2 = \int{\deltac}^{\delta{\max}} (P_3 - P_m) d\delta $

3.2 提高暂态稳定性的措施

1. 故障快速切除：减小加速面积
2. 自动重合闸：增加减速面积
3. 强行励磁：调节电磁功率
4. 快速关闭汽门：限制机械功率
5. 电气制动：消耗多余能量

3.3 暂态稳定性提高方向

• 优化保护系统动作时间
• 应用FACTS设备
• 动态无功补偿

---

参考文献

[1] 付兴贺, 陈锐. 电机中ABC到dq0坐标变换的梳理与辨析[J]. 微特电机, 2021.
[2] 田铭兴等. 交流电机坐标变换理论的研究[J]. 西安交通大学学报, 2002.
[3] IEEE Standard for Power System Stability Analysis. IEEE Xplore.