三相系统坐标变换分析与Park变换原理总结

摘要

Park变换是一种核心数学工具，广泛应用于电机控制和电力系统分析中。通过将三相静止坐标系（ABC坐标系）转换为同步旋转坐标系（dq0坐标系），Park变换有效简化了交流系统的动态特性分析和控制设计。本文详细探讨了Park变换的基本原理，包括坐标长度法和能量守恒法两种变换方法，并深入分析了变换后电机磁链和电压方程的数学推导过程。通过对比不同方法的特性，验证了Park变换在能量守恒性、数学简化及控制便利性方面的优势，为电机矢量控制提供了理论依据与技术支持。

关键词：Park变换；dq0坐标系；坐标长度法；能量守恒法；磁链方程；电压方程；电机控制

一、引言

Park变换是电机控制与电力系统分析中的核心工具，通过数学坐标变换，将三相交流系统（ABC坐标系）转换为两相同步旋转坐标系（dq0坐标系），从而简化系统分析与控制。逆Park变换则实现了从dq0坐标系回到ABC坐标系的转换。

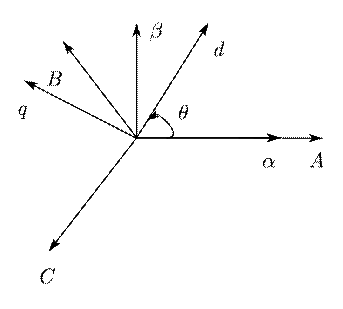
通过直接Park变换，三相电压、电流可以转换为dq0坐标系中的直轴分量$d$、交轴分量$q$和零序分量$0$。其中$d$轴与转子磁场方向对齐，$q$轴与$d$轴垂直，$q$轴超前$d$轴90度，如下图所示。

在三相系统中，$a$、$b$、$c$三相电压与电流通常呈平衡状态，三相幅值相同且相位相差120度。Clarke变换完成了三相到两相（$abc$到$\alpha\beta$）的变换，而Park变换在此基础上将固定坐标系（$\alpha\beta$）转换为旋转坐标系（$dq$），为交流系统的动态分析与控制提供了更直观且简化的数学描述。

坐标变换角度$\theta$定义明确对正确理解ABC与dq0坐标系之间的旋转关系非常重要，是分析电机稳态与动态特性的关键因素¹。此外，相关变换公式存在不同变体，如第三列系数的处理方式存在差异，需结合实际应用合理选取。这一变换简化了复杂电机控制问题，为系统建模与仿真提供了有效工具。

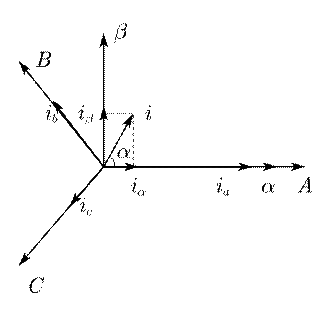
坐标长度法变换关系图：

二、正文

2.1 Park变换的含义

Park变换（也称为$dq0$变换）， Park 变换，也称为 dq0 变换，是一种用于分析三相交流系统（例如三相电机、电力系统）的数学工具。它的主要作用是将三相时变的交流量（例如电压、电流）转换为两相（或三相）时不变的直流或准直流分量。这种转换简化了对交流系统的分析和控制。从空间解析几何和矢量代数角度来看是同一空间矢量在不同空间三维坐标系中坐标表示的变换; 从系统控制论来看是系统状态方程的等价变换。从物理意义上来看是参照物的变换²。

2.2 坐标长度法

坐标长度法的核心思想是将三相交流量（如电压或电流）表示为空间矢量，并将其投影到同步旋转的$dq$坐标轴上。从而获取$dq$分量。在这一过程中，空间矢量在$dq$轴上的投影长度即为“坐标长度”，该方法基于幅值相等和等效旋转磁场原则，确保变换前后综合矢量的幅值保持不变³^,⁴。

三相电流表达式为：

$\begin{cases} i_a = I \cos \alpha \\ i_b = -I \cos (\alpha - 120^\circ) \\ i_c = -I \cos (\alpha + 120^\circ) \end{cases} \tag{1}$

变换矩阵为：

$i_{\alpha \beta \gamma}\left( t \right) =Ti_{abc}\left( t \right) =\frac{2}{3}\left[ \begin{matrix} 1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\\ \end{matrix} \right] \left[ \begin{array}{c} i_a\left( t \right)\\ i_b\left( t \right)\\ i_c\left( t \right)\\ \end{array} \right]\tag{2}$

在$dq$坐标系中，$d$轴为实轴，$q$轴为虚轴，该坐标系相对于三相$abc$坐标系以角度$θ$进行旋转。如上坐标长度法变换关系图，通过空间矢量投影，$d$轴分量对应空间矢量在$d$轴上的投影（复数表示的实部），$q$轴分量对应空间矢量在$q$轴上的投影（复数表示的虚部），而零序分量则代表三相电流的平均值，为三相电流向量和的1/3。在$dq$坐标系中，$d$轴分量$i_d$和$q$轴分量$i_q$分别为：

$\begin{cases} i_d = I \cos (\theta - \alpha) \\ i_q = -I \sin (\theta - \alpha) \end{cases} \tag{3}$

将固定坐标系转换为旋转坐标系，代入(2)式可得(4)(5)。

$\left\{ \begin{array}{l} i_d=i_{\alpha}\cos \theta +i_{\beta}\sin \theta\\ i_q=i_{\alpha}\cos \theta +i_{\beta}\sin \theta\\ \end{array} \right.\tag{4}$ $\left[ \begin{array}{c} i_d\\ i_q\\ i_o\\ \end{array} \right] =\left[ \begin{matrix} \cos \theta& \sin \theta& 0\\ -\sin \theta& \cos \theta& 0\\ 0& 0& 1\\ \end{matrix} \right] \left[ \begin{array}{c} i_{\alpha}\\ i_{\beta}\\ i_{\gamma}\\ \end{array} \right] =\left[ \begin{matrix} \cos \theta& \sin \theta& 0\\ -\sin \theta& \cos \theta& 0\\ 0& 0& 1\\ \end{matrix} \right] \cdot \frac{2}{3}\left[ \begin{matrix} 1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\\ \end{matrix} \right] \left[ \begin{array}{c} i_a\\ i_b\\ i_c\\ \end{array} \right]\tag{5}$

变换后最终结果如式(6)，得出P矩阵如(7)，和Park推导的结果一致⁵。

$i_{dq0}=Pi_{abc}=\frac{2}{3}\left[ \begin{matrix} \cos \theta& \cos \left( \theta -120^° \right)& cos\left( \theta +120^° \right)\\ -\sin \theta& -\sin \left( \theta -120^° \right)& -\sin \left( \theta +120^° \right)\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\\ \end{matrix} \right] \left[ \begin{array}{c} i_a\\ i_b\\ i_c\\ \end{array} \right]\tag{6}$ $P=\frac{2}{3}\left[ \begin{matrix} \cos \theta& \cos \left( \theta -120^° \right)& cos\left( \theta +120^° \right)\\ -\sin \theta& -\sin \left( \theta -120^° \right)& -\sin \left( \theta +120^° \right)\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\\ \end{matrix} \right]\tag{7}$

2.3 能量守恒法

Park 变换及其逆变换是一种理想的坐标变换，即变换过程不引入额外的能量损耗或产生能量增益。能量守恒法坐标变换即依据功率相等进行坐标变换。区别于上面等幅值变换,在使用等功率变换矩阵时，需注意保持变换前后系统的功率不变²。
上面“坐标长度法”变换后的电流 $i_d$、$i_q$ 、$i_0 $分量的幅值会与原始电流$ i_a$、$i_b $、$i_c $有一定的缩放关系，因此会引入一个系数，导致瞬时功率不直接守恒。
在理想的 Park 变换中，从能量守恒的角度考虑，瞬时功率应当保持不变。这意味着，三相系统在$ abc$ 坐标系中的瞬时功率，应该等于在 $dq0$ 坐标系中的瞬时功率。
电机系统的电压和电流，经过上述等幅值的变换后，实功和虚功会和原系统会差一个系数，原因是因为Clarke变换的矩阵不是酉矩阵（unitary matrix)。若要让实功和虚功的值在变换前后相同，需要用式(8)变换⁶。

$i_{\alpha \beta \gamma}\left( t \right) =Ti_{abc}\left( t \right) =\sqrt{\frac{2}{3}}\left[ \begin{matrix} 1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \end{matrix} \right] \left[ \begin{array}{c} i_a\left( t \right)\\ i_b\left( t \right)\\ i_c\left( t \right)\\ \end{array} \right]\tag{8}$

应用正交相似变换方法,通过引入缩放因子$\sqrt{\frac{2}{3}}$，确保变换前后的瞬时功率保持不变。能量守恒法修正后的Park得出的P矩阵如式(9)。

$P' = \sqrt{\frac{2}{3}} \begin{bmatrix} \cos\theta & \cos(\theta-120^\circ) & \cos(\theta+120^\circ) \\ -\sin\theta & -\sin(\theta-120^\circ) & -\sin(\theta+120^\circ) \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \tag{9}$

与上面等幅值变换得出的P矩阵不同，这里变换后定子和转子间的互感系数对称，是正交矩阵。

使用“能量守恒法”变换的优点：

物理一致性：瞬时功率守恒，数学模型与物理系统一致。

控制便利：$dq$分量直接用于矢量控制。

2.4 Park变换后的磁链和电压方程

2.4.1 磁链方程

磁链方程描述了电机绕组中磁链的变化与电流、磁场之间的关系。通过Park变换，磁链的三相分量被投影到旋转坐标系，形成了磁链的$dq0$分量。这种转换使得磁链方程中的自感和互感关系变得对称，同时磁链与电压、电流之间的关系变得更易于分析和控制。特别是在稳态条件下，$dq$分量中的磁链通常表现为恒定值，从而简化了电机的磁场定向控制（FOC）设计。三相绕组的磁链方程为式(10)所示。

$\left[ \begin{array}{c} \psi _{abc}\\ \psi _{fdq}\\ \end{array} \right] =\left[ \begin{matrix} L_{ss}& L_{sr}\\ L_{rs}& L_{rr}\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right]\tag{10}$

在等式两边同时左乘 $\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right]$ ，其中$U$为三阶单位矩阵。

$\left[ \begin{array}{c} \psi _{dq0}\\ \psi _{fdq}\\ \end{array} \right] =\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{array}{c} \psi _{abc}\\ \psi _{fdq}\\ \end{array} \right] \tag{11}$ $\left[ \begin{array}{c} \psi _{dq0}\\ \psi _{fdq}\\ \end{array} \right] =\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{matrix} L_{ss}& L_{sr}\\ L_{rs}& L_{rr}\\ \end{matrix} \right] \left[ \begin{matrix} P^{-1}& 0\\ 0& U^{-1}\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right]$ $\left[ \begin{array}{c} \psi _{dq0}\\ \psi _{fdq}\\ \end{array} \right] =\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{matrix} L_{ss}& L_{sr}\\ L_{rs}& L_{rr}\\ \end{matrix} \right] \left[ \begin{matrix} P^{-1}& 0\\ 0& U^{-1}\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right]$ $=\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{matrix} L_{ss}& L_{sr}\\ L_{rs}& L_{rr}\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right] \left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{matrix} L_{ss}& L_{sr}\\ L_{rs}& L_{rr}\\ \end{matrix} \right] \left[ \begin{matrix} P^{-1}& 0\\ 0& U^{-1}\\ \end{matrix} \right] \left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right]\tag{12}$

最终得出式(13)。

$\left[ \begin{array}{c} \psi _{dq0}\\ \psi _{fdq}\\ \end{array} \right] =\left[ \begin{matrix} PL_{ss}P^{-1}& PL_{sr}\\ L_{rs}P^{-1}& L_{rr}\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right]\tag{13}$

2.4.2 电压方程

在电机控制理论中，Park变换将三相静止坐标系中的电压分量转换到旋转坐标系中的$dq0$分量。通过这种变换，三相电压的正弦量被简化为直流量（在稳态条件下），从而使控制系统更易于分析和实现。在旋转坐标系中，电压方程包含定子电阻压降、电感电压及反电动势项，其表现形式更加清晰，并能够直接反映电压与电流之间的关系，有助于对电机进行稳态和动态特性的分析。三相绕组的电压方程为式(14)所示。

$\left[ \begin{array}{c} u_{abc}\\ u_{fdq}\\ \end{array} \right] =\left[ \begin{matrix} R_s& 0\\ 0& R_r\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right] +\left[ \begin{array}{c} \dot{\psi}_{abc}\\ \dot{\psi}_{fdq}\\ \end{array} \right]\tag{14}$

在等式两边同时左乘 $\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right]$ ，其中$U$为三阶单位矩阵。

$\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{array}{c} u_{abc}\\ u_{fdq}\\ \end{array} \right] =\left[ \begin{array}{c} u_{dq0}\\ u_{fdq}\\ \end{array} \right]\tag{15}$ $\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{matrix} R_s& 0\\ 0& R_r\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right] =\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{matrix} R_s& 0\\ 0& R_r\\ \end{matrix} \right] \left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] ^{-1}\left[ \begin{matrix} P& 0\\ 0& U\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right]$ $=\left[ \begin{matrix} R_s& 0\\ 0& R_r\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{abc}\\ i_{fdq}\\ \end{array} \right]\tag{16}$

最终得出式(17)。

$\left[ \begin{array}{c} u_{dq0}\\ u_{fdq}\\ \end{array} \right] =\left[ \begin{matrix} R_s& 0\\ 0& R_r\\ \end{matrix} \right] \left[ \begin{array}{c} -i_{dq0}\\ i_{fdq}\\ \end{array} \right] +\left[ \begin{array}{c} P\dot{\psi}_{abc}\\ \dot{\psi}_{fdq}\\ \end{array} \right]\tag{17}$

三、总结

本文系统地分析了Park变换在电机控制与电力系统中的应用。

首先，基于坐标长度法，本文推导了三相系统向$dq0$坐标系的变换关系，解释了其物理意义及数学特性。其次，针对能量守恒法，讨论了功率一致性的重要性，并通过修正变换矩阵，确保了瞬时功率的守恒。最后，结合电机磁链方程和电压方程的推导，验证了Park变换在简化复杂电机模型中的有效性。

通过Park变换，三相交流系统的非线性正弦量被转换为易于分析的直流或准直流量，从而显著简化了电机控制系统的设计过程。这一工具不仅提供了清晰的数学描述，也为电机的矢量控制和稳态分析提供了理论支撑。总体而言，Park变换是电力电子领域中不可或缺的数学工具，对于提升电机系统的性能与控制精度具有重要意义。

四、参考文献

¹:付兴贺, 陈锐. 电机中ABC到dq0坐标变换的梳理与辨析[J]. 微特电机, 2021.
²:田铭兴等. 交流电机坐标变换理论的研究[J]. 西安交通大学学报, 2002.
³: Pulse Width Modulation for Power Converters: Principles and Practice. IEEE Xplore.
⁴: 王佑民, 孙进, 乔波强. 基于PARK变换下的矩阵变换器分析[J]. 电机与控制应用, 2012(S1): 16-20.
⁵: PARK R H. Two-reaction theory of synchronous machines generalized method of analysis-part I[J/OL]. Transactions of the American Institute of Electrical Engineers, 1929, 48(3): 716-727. DOI:10.1109/T-AIEE.1929.5055275.
⁶: Area Based Approach for Three Phase Power Quality Assessment in Clarke Plane[EB/OL]. [2024-12-15]. https://www.researchgate.net/publication/26500171_Area_Based_Approach_for_Three_Phase_Power_Quality_Assessment_in_Clarke_Plane.