电力系统短路计算总结与两相短路故障分析

摘要

本文探讨了电力系统中对称与不对称短路故障的分析方法与计算原理。基于对称分量法，分解故障为正序、逆序和零序三套系统，分别建立序网方程并分析其特性。本文重点分析了两相短路故障的边界条件、等效电路以及故障点电压和电流的计算过程，得到了相关电压、电流相量关系及故障分析的关键步骤。研究结果为深入理解电力系统故障特性及优化设计提供了帮助。

关键词：电力系统；短路故障；对称分量法；序网分析；两相短路

一、电力系统短路计算原理和方法总结

1. 对称短路

短路后达到新的三相对称状态，只需列出单相的KVL方程，得到关于电流的一阶微分方程并求解。另外两项通过相位调整即可获得。

2. 不对称短路

将故障部分根据戴维南等值为接入了一个不对称的带内阻的电压源。利用对称分量法，将不对称的系统分解为三套对称的系统，分别为正序、逆序、零序系统$𝐼𝑎$、$𝐼𝑏$、$𝐼_𝑐$代表不对称的三相电流，可分解为：

$\begin{cases} \dot{I}_a=\dot{I}_{a1}+\dot{I}_{a2}+\dot{I}_{a0}\\ \dot{I}_b=\dot{I}_{b1}+\dot{I}_{b2}+\dot{I}_{b0}\\ \dot{I}_c=\dot{I}_{c1}+\dot{I}_{c2}+\dot{I}_{c0}\\ \end{cases}$

各序分量关系为：

${} \begin{cases} \dot{I}_{b1}=\dot{I}_{a1}e^{-j120^°},\dot{I}_{c1}=\dot{I}_{a1}e^{j120^°}\\ \dot{I}_{b2}=\dot{I}_{a2}e^{j120°},\dot{I}_{c2}=\dot{I}_{a2}e^{-j120°}\\ \dot{I}_{a0}=\dot{I}_{b0}=\dot{I}_{c0}\\ \end{cases}$

对三个系统的单项电路进行分析，其中仅有正序网络有电源，这是由发电机本身的绕组相序决定的。

正序单项等效电路图和序网方程分别为

$\dot{U}_{a1}=\dot{E}_a-\dot{I}_{a1}\text{（}Z_{G1}+Z_{I1}\text{）}$

逆序单相等效电路图和序网方程分别为

$\dot{U}_{a2}=0-\dot{I}_{a2}\text{（}Z_{G2}+Z_{I2}\text{）}$

零序单相等效电路图和序网方程分别为

$\dot{U}_{a0}=0-\dot{I}_{a0}\left( Z_{G0}+Z_{l0}+Z_n \right)$

三套对称系统的分析计算只需分析一相即可把该相定为基准相，依据上述的序网方程列出方程组

$\left\{ \begin{array}{l} \dot{U}_{k1}=\dot{E}_{\varSigma}-j\dot{I}_{k1}X_{\varSigma 1}\\ \dot{U}_{k2}=-j\dot{I}_{k2}X_{\varSigma 2}\\ \dot{U}_{k0}=-j\dot{I}_{k0}X_{\varSigma 0}\\ \end{array} \right.$

此外还需要列出不对称故障系统的边界条件，可揭示不同序网之间的内在联系。

不对称电力系统分析步骤：

确定基准相

列出边界条件

变换为计算分析条件

计算故障电压和电流

二、两相短路的故障点电压和电流计算

以a相为基准，bc两相短路的边界条件为：

$\begin{cases} \dot{I}_a = 0 \\ \dot{I}_b = -\dot{I}_c \\ \dot{U}_b = \dot{U}_c \end{cases}$

通过对称分量法转换到a相分析：

$\left\{ \begin{array}{l} \dot{I}_{a1}+\dot{I}_{a2}+\dot{I}_{a0}=0\\ a^2\dot{I}_{a1}+a\dot{I}_{a2}+\dot{I}_{a0}=-\left( a\dot{I}_{a1}+a^2\dot{I}_{a2}+\dot{I}_{a0} \right)\\ a^2\dot{U}_{a1}+a\dot{U}_{a2}+\dot{U}_{a0}=a\dot{U}_{a1}+a^2\dot{U}_{a2}+\dot{U}_{a0}\\ \end{array} \right.$

化简后得到：

$\left\{ \begin{array}{l} I_{a1}+I_{a2}+I_{a0}=0& \\ U_{a1}=U_{a2}& \\ I_{a1}=-I_{a2}\text{，}I_{a0}=0\text{，}U_{a0}=0& \end{array} \right.$

物理意义：

$I_{a1} + I_{a2} + I_{a0} = 0$ ：正序、负序、零序电流首尾共节点
$U_{a1} = U_{a2}$ ：正序与负序电压首端同电位
$I_{a0} = 0$ ：零序电流断路

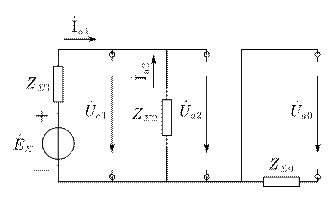
画出等效电路图:

故障电流计算：

$I_{a1} = \frac{E_\Sigma}{Z_{\Sigma 1} + Z_{\Sigma 2}}$ $I_b = \left( a^2 - a \right) I_{a1} = -j \sqrt{3} \frac{E_\Sigma}{Z_{\Sigma 1} + Z_{\Sigma 2}}$ $I_c = -I_b = j \sqrt{3} \frac{E_\Sigma}{Z_{\Sigma 1} + Z_{\Sigma 2}}$

故障电压计算：

$U_{a1} = U_{a2} = \frac{1}{2} E_\Sigma$ $U_a = U_{a1} + U_{a2} + U_{a0} = E_\Sigma$ $U_b = U_c = \left( a^2 + a \right) U_{a1} = -\frac{1}{2} E_\Sigma$

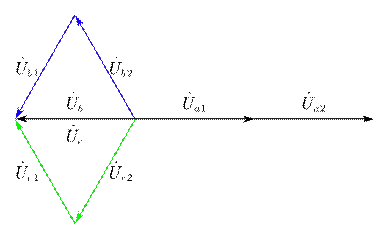
两相短路电压相量图: